
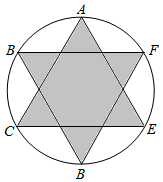
 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$. 分析 设圆的半径为1,则正六边形的边长为1由题意知本题是一个几何概型,试验发生包含的所有事件是阴影部分面积,而满足条件的阴影区域是正六边形的面积的$\frac{2}{3}$,根据概率公式计算即可.
解答  解:设圆的半径为1,则正六边形的边长为1,其面积为$\frac{3\sqrt{3}}{2}$,
解:设圆的半径为1,则正六边形的边长为1,其面积为$\frac{3\sqrt{3}}{2}$,
如图将整个正六边形分割成了3×6=18个小三角形,那么整个阴影面积是正六边形的面积的$\frac{12}{18}$=$\frac{2}{3}$,故S阴影=$\frac{3\sqrt{3}}{2}$×$\frac{2}{3}$=$\sqrt{3}$,
圆的面积为S圆=π,
故圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$,
故答案为:1-$\frac{\sqrt{3}}{π}$.
点评 本题考查几何概型、等可能事件的概率,且把几何概型同几何图形的面积结合起来,几何概型和古典概型是高中必修中学习的,高考时常以选择和填空出现,有时文科会考这种类型的解答.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{4}{3}$)∪(2,+∞) | B. | (-$\frac{4}{3}$,2) | C. | (-∞,$\frac{4}{3}$)∪(2,+∞) | D. | ($\frac{4}{3}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 120 | C. | 300 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 72种 | C. | 144种 | D. | 288种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com