
分析 根据二项式展开式的通项公式,令展开式中含x项的指数等于3,求出r的值,即可求出展开式中x3项的系数.
解答 解:二项式(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6展开式的通项公式为
Tr+1=${C}_{6}^{r}$•${(2\sqrt{x})}^{6-r}$•${(-\frac{1}{\sqrt{x}})}^{r}$=(-1)r•26-r•${C}_{6}^{r}$•x3-r,
令3-r=3,
解得r=0;
∴展开式中x3项的系数是26×${C}_{6}^{0}$=64.
故答案为:64.
点评 本题考查了利用二项式展开式的通项公式求展开式中特定项的系数问题,是基础题目.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,log3x≤0 | B. | ¬p:?x∈R,log3x≤0 | C. | ¬p:?x∈R,log3x<0 | D. | ¬p:?x∈R,log3x<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 3 | -2 | 1 | 5 | m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5) | B. | (-5.25,-5) | C. | [-5.25,-5) | D. | 前三个都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | ±$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
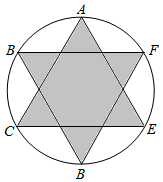 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com