
分析 析:(1)圆心到直线的距离求半径.(2)由|PO|2=|PA|.|PB|平方化简得x2-y2=2,注意曲线是已知圆的内部.
解答 解:(Ⅰ) 依题设,圆O的半径r等于原点O到直线$x-\sqrt{3}y-4=0$的距离,
则$r=\frac{4}{{\sqrt{1+3}}}=2$,
得圆O的方程为x2+y2=4…(5分)
(Ⅱ)不妨设A(x1,0),B(x2,0),x1<x2,
由x2=4即得A(-2,0),B(2,0),
设P(x,y),由|PA|,|PO|,|PB|成等比数列得,$\sqrt{{{(x-2)}^2}+{y^2}}•\sqrt{{{(x-2)}^2}-{y^2}}={x^2}+{y^2}$,
即x2-y2=2…(9分)
由于点P在圆O内,故$\left\{\begin{array}{l}{x^2}+{y^2}<4\\{x^2}-{y^2}=2\end{array}\right.$
由此得$-\sqrt{3}<x≤-\sqrt{2}$或$\sqrt{2}≤x<\sqrt{3}$
所以所求轨迹方程为x2-y2=2($-\sqrt{3}<x≤-\sqrt{2}$或$\sqrt{2}≤x<\sqrt{3}$)…(11分)
即P点的轨迹为双曲线x2-y2=2
在圆x2+y2=4内的一部分…(12分)
点评 本题考查了直接法来求轨迹方程,平方化简是一个难点.对于题中条件“圆内O的定点P”这一条件要审清.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,α∥β,则a∥β | C. | 若a⊥c,b⊥c,则a∥b | D. | 若a⊥α,b⊥α,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
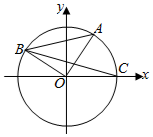 如图,A,B,C是单位圆O上的点,且A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),C是圆O与x轴正半轴的交点,∠AOB=90°.
如图,A,B,C是单位圆O上的点,且A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),C是圆O与x轴正半轴的交点,∠AOB=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2-$\frac{1}{3}$ | B. | y=3x2-$\frac{2}{3}$ | C. | y=2x2-$\frac{2}{3}$ | D. | y=$\frac{1}{2}$x2-$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com