
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,α∥β,则a∥β | C. | 若a⊥c,b⊥c,则a∥b | D. | 若a⊥α,b⊥α,则a∥b |
分析 根据直线与平面之间的位置关系,平面与平面之间的位置关系,分别进行判断,即可得出结论.
解答 解:对于A,∵a∥α,b∥α,∴当a,b共面时,满足a∥b或a,b相交,当a,b不共面时,a和b为异面直线,∴a和b的关系是平行、相交或异面.即A不正确;
对于B,若a∥α,α∥β,则a∥β或a?β.即B不正确;
对于C,若a⊥c,b⊥c,则a∥b或相交或异面,即C不正确;
对于D,若a⊥α,b⊥α,根据垂直于同一平面的两条直线平行,可得a∥b,正确.
故选:D.
点评 本题考查的知识点是空间直线与直线之间的位置关系,直线与平面之间的位置关系,平面与平面之间的位置关系,熟练掌握空间线面之间的位置关系的定义,几何特征及判定方法是解答的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
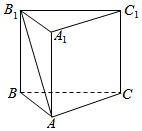 如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.
如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某隧道的截面图由矩形ABCD和抛物线型拱顶DEC组成(E为拱顶DEC的最高点),以AB所在直线为x轴,以AB的中点为坐标原点,建立平面直角坐标系xOy,已知拱顶DEC的方程为y=-$\frac{1}{4}$x2+6(-4≤x≤4).
如图,某隧道的截面图由矩形ABCD和抛物线型拱顶DEC组成(E为拱顶DEC的最高点),以AB所在直线为x轴,以AB的中点为坐标原点,建立平面直角坐标系xOy,已知拱顶DEC的方程为y=-$\frac{1}{4}$x2+6(-4≤x≤4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
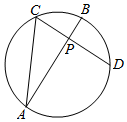 如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )
如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )| A. | 5 | B. | $\sqrt{35}$ | C. | $\sqrt{30}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x-π)一定是奇函数 | B. | f(x-π)一定是偶函数 | ||
| C. | f(x+π)一定是奇函数 | D. | f(x+π)一定是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com