
分析 (Ⅰ)利用三角恒等变换化简函数f(x)的解析式,从而求得f($\frac{π}{6}$)的值.
(Ⅱ)根据f(x)的解析式,利用正弦函数的单调性,求得函数的单调增区间.
(Ⅲ)根据α∈(0,π),以及三角函数在各个象限中的符号,求得cos(α+$\frac{π}{3}$)的值,利用两角和的正弦公式可得sin(α+$\frac{7π}{12}$)的值.
解答 解:(Ⅰ)∵函数f(x)=$\sqrt{3}$cos2x+sinxcosx=$\frac{\sqrt{3}}{2}(1+cos2x)$+$\frac{1}{2}$sin2x=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,∴f($\frac{π}{6}$)=sin$\frac{2π}{3}$+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
(Ⅱ)∵f(x)=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得 kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,
可得函数的增区间为:$[kπ-\frac{5π}{12},kπ+\frac{π}{12}],k∈Z$.
(Ⅲ)∵$f(\frac{α}{2})=\frac{{\sqrt{3}}}{2}+sin(α+\frac{π}{3})=\frac{1}{4}+\frac{{\sqrt{3}}}{2}$,∴$sin(α+\frac{π}{3})=\frac{1}{4}$,因为α∈(0,π),∴$α+\frac{π}{3}∈(\frac{π}{3}$,$\frac{4π}{3})$.
若$α+\frac{π}{3}∈(\frac{π}{3},\frac{π}{2})$,则$sin(α+\frac{π}{3})>\frac{{\sqrt{3}}}{2}$,矛盾,又$sin(α+\frac{π}{3})=\frac{1}{4}$,所以$α+\frac{π}{3}∈(\frac{π}{2},π)$,$cos(α+\frac{π}{3})=-\frac{{\sqrt{15}}}{4}$,
∴$sin(α+\frac{7π}{12})=sin(α+\frac{π}{3}+\frac{π}{4})$=$\frac{{\sqrt{2}}}{2}[sin(α+\frac{π}{3})+cos(α+\frac{π}{3})]=\frac{{\sqrt{2}-\sqrt{30}}}{8}$.
点评 本题主要考查三角恒等变换,正弦函数的单调性,以及三角函数在各个象限中的符号,两角和的正弦公式,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {1,0} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0.1% | B. | 1% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
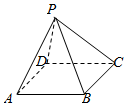 如图,四棱锥P-ABCD的底面ABCD是棱长为2的菱形,∠DAB=$\frac{π}{3}$,侧面PAD为等边三角形,PB=$\sqrt{3}$
如图,四棱锥P-ABCD的底面ABCD是棱长为2的菱形,∠DAB=$\frac{π}{3}$,侧面PAD为等边三角形,PB=$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}<a<1$ | B. | $\frac{1}{2}≤a<1$ | C. | 1<a≤2 | D. | 1<a<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | -36 | -15 | -3 | 10 | -32 | -52 |
| A. | (1,2)和(2,3) | B. | (2,3)和(3,4) | C. | (3,4)和(4,5) | D. | (4,5)和(5,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,α∥β,则a∥β | C. | 若a⊥c,b⊥c,则a∥b | D. | 若a⊥α,b⊥α,则a∥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com