练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．某校为了研究“学生的性别”和“对待某项运动的喜爱程度”是否有关，运用2×2列联表进行独立性检验，经计算k=6.669，则认为“学生性别与支持活动有关系”的犯错误的概率不超过（　　）
    附：
    P（K2≥k0） 0.1000.0500.0250.0100.001
    k02.706 3.8415.0246.63510.828
    A．0.1%B．1%C．99%D．99.9%

    分析 把观测值同临界值进行比较．得到“学生性别与支持活动有关系”的犯错误的概率．

    解答 解：因为K2=6.669＞6.635，对照表格：

    P（k2≥k0）0.1000.0500.0250.0100.001
    k02.7063.8415.0246.63510.828
    所以认为“学生性别与支持活动有关系”的犯错误的概率不超过1%．
    故选：B．

    点评 本题考查独立性检验知识的运用，正确对照临界值表是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．在斜三角形△ABC中，A=45°，H是△ABC的垂心，λ$\overrightarrow{AH}$=$\frac{\overrightarrow{AB}}{tanC}$+$\frac{\overrightarrow{AC}}{tanB}$，则λ=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．某县农民的月收入ξ服从正态分布N（1000，402），则此县农民中月收入在1000元到1080元间的人数的百分比为47.72%．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=|x2-1|
    （1）解不等式f（x）≤2+2x；
    （2）设a＞0，若关于x的不等式f（x）+5≤ax解集非空，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

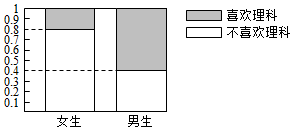
    20．如图是调查某地区男女中学生是否喜欢理科的等高条形图，从如图可以看出该地区的中学生（　　）
    A．性别与是否喜欢理科无关B．女生中喜欢理科的比为80%
    C．男生比女生喜欢理科的可能性大D．男生中喜欢理科的比例为80%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．直线y=kx-k与抛物线y2=4x交于A，B两点，若|AB|=4，则弦AB的中点到y轴的距离为（　　）
    A．$\frac{3}{4}$B．1C．2D．$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=$\sqrt{3}$cos2x+sinxcosx．
    （Ⅰ）求f（$\frac{π}{6}$）的值；
    （Ⅱ）求f（x）的单调增区间；
    （Ⅲ）若α∈（0，π），f（$\frac{α}{2}$）=$\frac{1}{4}$+$\frac{{\sqrt{3}}}{2}$，求sin（α+$\frac{7π}{12}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在极坐标系中，关于曲线C：ρ=4sin（θ-$\frac{π}{3}$）的下列判断中正确的是（　　）
    A．曲线C关于点（2，$\frac{π}{3}$）对称B．曲线C关于极点（0，0）对称
    C．曲线C关于直线θ=$\frac{5π}{6}$对称D．曲线C关于直线θ=$\frac{π}{3}$对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图，某隧道的截面图由矩形ABCD和抛物线型拱顶DEC组成（E为拱顶DEC的最高点），以AB所在直线为x轴，以AB的中点为坐标原点，建立平面直角坐标系xOy，已知拱顶DEC的方程为y=-$\frac{1}{4}$x2+6（-4≤x≤4）．
    （1）求tan∠AEB的值；
    （2）现欲在拱顶上某点P处安装一个交通信息采集装置，为了获得最佳采集效果，需要点P对隧道底AB的张角∠APB最大，求此时点P到AB的距离．

    查看答案和解析>>

    同步练习册答案