练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．直线y=kx-k与抛物线y2=4x交于A，B两点，若|AB|=4，则弦AB的中点到y轴的距离为（　　）
    A．$\frac{3}{4}$B．1C．2D．$\frac{4}{3}$

    分析 确定抛物线的准线方程，利用抛物线的定义及弦长，可得弦AB的中点到准线的距离，进而可求弦AB的中点到y轴的距离．

    解答 解：由题意，直线y=kx-k恒过（1，0），
    抛物线y2=4x的焦点坐标为（1，0），准线方程为x=-1，
    根据抛物线的定义，∵|AB|=4，∴A、B到准线的距离和为4，
    ∴弦AB的中点到准线的距离为2
    ∴弦AB的中点到y轴的距离为2-1=1
    故选：B．

    点评 本题考查抛物线的定义，考查学生的计算能力，正确运用抛物线的定义是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．一个总体中有60个个体，随机编号为0，1，2，…59，依编号顺序平均分成6个小组，组号依次为1，2，3，…6．现用系统抽样方法抽取一个容量为6的样本，若在第1组随机抽取的号码为3，则在第5组中抽取的号码是（　　）
    A．33B．43C．53D．54

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．非齐次线性方程组AX=B的解向量是ξ1，ξ2，…ξt，若k1ξ1+k2ξ2+…+ktξt也是AX=B的解，则k1+k2+…+kt=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（　　）
    A．若Χ2的观测值为6.64，而P（Χ2≥6.64）=0.010，故我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病
    B．从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病
    C．若从统计量中求出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推判出现错误
    D．以上三种说法都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．某校为了研究“学生的性别”和“对待某项运动的喜爱程度”是否有关，运用2×2列联表进行独立性检验，经计算k=6.669，则认为“学生性别与支持活动有关系”的犯错误的概率不超过（　　）
    附：
    P（K2≥k0） 0.1000.0500.0250.0100.001
    k02.706 3.8415.0246.63510.828
    A．0.1%B．1%C．99%D．99.9%

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

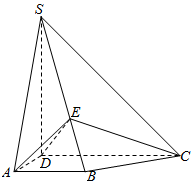    15．如图，四棱锥S-ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC⊥平面SBC．
    （Ⅰ）求$\frac{SE}{EB}$的值；
    （Ⅱ）求二面角A-DE-C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知：f（x）=$\sqrt{{x}^{2}+2}$，正项数列{an}中，a1=2，an+1=f（an），数列{bn}的前n项和为Sn，且满足an2=2n+1bn
    （1）求{bn}的通项公式
    （2）若不等式设2n•Sn＞m•2n-2an2对?n∈N+恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

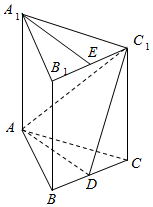    19．如图，在正三棱柱ABC-A1B1C1中，点D、E分别为BC、B1C1的中点，且AB=AA1=2．
    （1）求证：A1E⊥C1D；
    （2）求证：A1E∥平面AC1D；
    （3）求直线AC1与平面BCC1B1所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知复数z满足$\frac{1-i}{z-2}$=1+i，则在复平面内，复数z对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案