
分析 (Ⅰ)设出C,A的坐标,利用中点坐标公式把A的坐标用C的坐标表示,然后代入曲线方程求得动点C的轨迹方程;
(Ⅱ)假设存在点P(x0,y0),使得PM、PN分别为轨迹E的切线,设出M,N的坐标及直线MN的方程,联立直线方程与抛物线方程,得到M,N的横坐标的和与积,然后分别写出过M,N的切线方程,知x1,x2是方程${x_{\;}}^2-2{x_0}x+4{y_0}=0$的两根,进一步求得P的坐标,则可求得轨迹E与直线PM、PN所围成的图形的面积.
解答 解:(Ⅰ)设C(x,y),A(m,n),则$\left\{\begin{array}{l}2=\frac{x+m}{2}\\ 0=\frac{y+n}{2}\end{array}\right.$,
∴$\left\{\begin{array}{l}m=4-x\\ n=-y\end{array}\right.$,
又$n=-\frac{{{{(m-4)}^2}}}{4}$,
∴所求方程为x2=4y;
(Ⅱ)假设存在点P(x0,y0),使得PM、PN分别为轨迹E的切线,
设M(x1,y1),N(x2,y2),直线MN的方程为y=kx+1,
联立$\left\{\begin{array}{l}y=kx+1\\{x^2}=4y\end{array}\right.$,
得x2-4kx-4=0,
则$\left\{\begin{array}{l}{x_1}+{x_2}=4k\\{x_1}{x_2}=-4\end{array}\right.$,
切线PM的方程为$y-\frac{x_1^2}{4}=\frac{x_1}{2}(x-{x_1})$,
点P(x0,y0)代入化简得${x_1}^2-2{x_1}{x_0}+4{y_0}=0$.
同理得${x_2}^2-2{x_2}{x_0}+4{y_0}=0$,
知x1,x2是方程${x_{\;}}^2-2{x_0}x+4{y_0}=0$的两根,
则x1x2=4y0=-4.
∴y0=-1,代入圆方程得x0=0,
∴存在点P(0,-1).
此时轨迹E与直线PM、PN所围成的图形的面积:
S=$\frac{1}{2}×2×1+{2∫}_{0}^{2}\frac{1}{4}{x}^{2}dx$=1$+2×\frac{1}{12}{x}^{3}{|}_{0}^{2}=1+\frac{4}{3}=\frac{7}{3}$.
点评 本题考查曲线方程的求法,训练了交轨法求曲线方程,考查直线与圆锥曲线位置关系的应用,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [2,+∞) | C. | (-∞,1] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
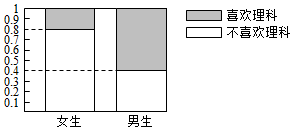
| A. | 性别与是否喜欢理科无关 | B. | 女生中喜欢理科的比为80% | ||
| C. | 男生比女生喜欢理科的可能性大 | D. | 男生中喜欢理科的比例为80% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
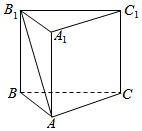 如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.
如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com