
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |
分析 设公差为d,运用等差数列的通项公式和等比数列的中项性质,解方程可得首项为1,公差为2,由分组求和即可得到所求和.
解答 解:公差d大于0的等差数列{an}中,2a7-a13=1,
可得2(a1+6d)-(a1+12d)=1,可得a1=1,
由a1,a3-1,a4+9成等比数列,
可得(a3-1)2=a1(a4+9),
即为 (1+2d-1)2=1(1+3d+9),
解得d=2(-$\frac{5}{4}$舍去).
则an=2n-1,
数列{(-1)n-1an}的前21项和为1-3+5-7+…+37-39+41
=-2×10+41=21.
故选:A.
点评 本题考查等差数列的通项公式,以及等比数列的中项的性质,考查方程思想,以及求和方法,考查运算能力,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
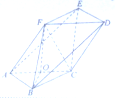 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)=x2+1 | B. | f(x)=sinx | C. | f(x)=2x | D. | f(x)=log2|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 10 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
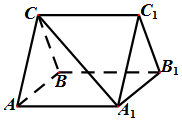 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α>β | B. | α<β | C. | α2>β2 | D. | α+β>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com