
分析 根据$\overrightarrow{AB}=-2\overrightarrow{AC}$便可得出三点A,B,C共线,然后可用有向线段表示出向量$\overrightarrow{AB},\overrightarrow{AC}$,这样根据图形即可判断每个描述的正误,从而写出描述正确的序号.
解答 解:$\overrightarrow{AB}=-2\overrightarrow{AC}$;
∴$\overrightarrow{AB},\overrightarrow{AC}$共线;
∴A,B,C三点共线,用有向线段表示如下:
∴只有②正确,三点共线,且点A在线段BC上.
故答案为:②.
点评 考查共线向量基本定理,以及向量数乘的几何意义,用有向线段表示向量的方法.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
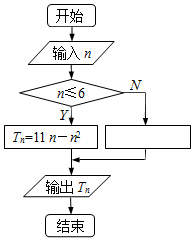 已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.
已知{an}是递减等差数列,如图是对数列{|an|}前n项和Tn求法的算法流程图,图中空白处理框中应填入${T_n}={n^2}-11n+60$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | [-2,-1) | C. | (-1,1) | D. | [-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com