
分析 可画出图形,然后分别过A,B作BC,AC的垂线AD,BE,垂足分别为D,E,根据三角形的面积公式便可得到:$|\overrightarrow{AB}||\overrightarrow{AC}|=|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}$,而由条件$\overrightarrow{AB}•\overrightarrow{AC}=3\overrightarrow{BA}•\overrightarrow{BC}$便可得到$|\overrightarrow{AB}||\overrightarrow{AC}|cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$,带入前面的式子即可得到$\frac{sinB}{sinA}•cosA=3cosB$,这样即可求出$\frac{tanA}{tanB}$的值.
解答 解:如图,过A作AD⊥BC,垂足为D,作BE⊥AC,垂足为E,则: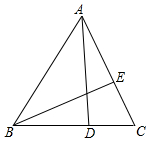
$|\overrightarrow{AB}|sinA•|\overrightarrow{AC}|=|\overrightarrow{BA}|sinB•|\overrightarrow{BC}|$;
∴$|\overrightarrow{AB}||\overrightarrow{AC}|=|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}$;
由$\overrightarrow{AB}•\overrightarrow{AC}=3\overrightarrow{BA}•\overrightarrow{BC}$得,$|\overrightarrow{AB}||\overrightarrow{AC}|cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$;
∴$|\overrightarrow{BA}||\overrightarrow{BC}|•\frac{sinB}{sinA}•cosA=3|\overrightarrow{BA}||\overrightarrow{BC}|cosB$;
∴$\frac{sinB}{sinA}•cosA=3cosB$;
∴$\frac{sinB}{cosB}=3•\frac{sinA}{cosA}$,即tanB=3tanA;
∴$\frac{tanA}{tanB}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 考查正弦函数的定义,三角形的面积公式,以及数量积的计算公式,弦化切公式.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
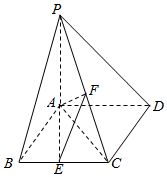 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A | B | C | D | E |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com