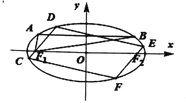
[题目]如图. 分别是椭圆的左.右焦点.焦距为.动弦平行于轴.且.(1)求椭圆的方程,(2)过分别作直线交椭圆于和.且.求四边形面积的最大值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，分别是椭圆的左、右焦点，焦距为，动弦平行于轴，且.

（1）求椭圆的方程；

（2）过分别作直线交椭圆于和，且，求四边形面积的最大值.

【答案】（1）；（2）4.

【解析】试题分析：（1）由椭圆的对称性及已知得，又因为，所以，从而得到椭圆方程；（2）讨论的倾斜角，利用根与系数的关系表示四边形面积，进而得到四边形面积的最大值.

试题解析：

（1）因为焦距，所以，

由椭圆的对称性及已知得，又因为

，所以，

因此，于是，

因此椭圆方程为；

（2）当的倾斜角为0°时，与重合，不满足题意

当的倾斜角不为0°时，由对称性得四边形为平行四边形

，设直线的方程为

代入，得

显然，设，，

则，

所以

设，所以，，

所以

当且仅当即时，即时等号成立。

所以，而

所以

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数（a＞0，a≠1，m≠﹣1），是定义在（﹣1，1）上的奇函数．

（I）求f（0）的值和实数m的值；

（II）当m=1时，判断函数f（x）在（﹣1，1）上的单调性，并给出证明；

（III）若且f（b﹣2）+f（2b﹣2）＞0，求实数b的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

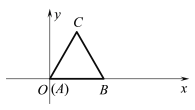
【题目】如图放置的边长为2的正三角形ABC沿x轴滚动，记滚动过程中顶点A的横、纵坐标分别为和，且是在映射作用下的象，则下列说法中：

① 映射的值域是；

② 映射不是一个函数；

③ 映射是函数，且是偶函数；

④ 映射是函数，且单增区间为，

其中正确说法的序号是___________.

说明：“正三角形ABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点B为中心顺时针旋转，当顶点C落在x轴上时，再以顶点C为中心顺时针旋转，如此继续．类似地，正三角形ABC可以沿x轴负方向滚动．

查看答案和解析>>

科目：高中数学 来源： 题型：

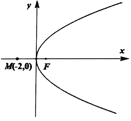
【题目】已知抛物线的焦点为，为过定点的两条直线.

（1）若与抛物线均无交点，且，求直线的斜率的取值范围；

（2）若与抛物线交于两个不同的点，以为直径的圆过点，求圆的方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设x，y∈R，则（3﹣4y﹣cosx）2+（4+3y+sinx）2的最小值为（）
A.4
B.5
C.16
D.25

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的离心率为，其左顶点A在圆O：x2+y2=16上．（Ⅰ）求椭圆W的方程；
（Ⅱ）若点P为椭圆W上不同于点A的点，直线AP与圆O的另一个交点为Q．是否存在点P，使得？若存在，求出点P的坐标；若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】四棱锥中，底面为直角梯形，，，，，，且平面平面．

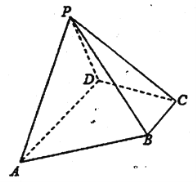
（1）求证：；

（2）在线段上是否存在一点，使二面角的大小为，若存在，求出的值；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系上，有一点列P0 ， P1 ， P2 ， P3 ， …，Pn﹣1 ， Pn ，设点Pk的坐标（xk ， yk）（k∈N，k≤n），其中xk、yk∈Z，记△xk=xk﹣xk﹣1 ， △yk=yk﹣yk﹣1 ，且满足|△xk||△yk|=2（k∈N* ， k≤n）；
（1）已知点P0（0，1），点P1满足△y1＞△x1＞0，求P1的坐标；
（2）已知点P0（0，1），△xk=1（k∈N* ， k≤n），且{yk}（k∈N，k≤n）是递增数列，点Pn在直线l：y=3x﹣8上，求n；
（3）若点P0的坐标为（0，0），y2016=100，求x0+x1+x2+…+x2016的最大值．