
如图五面体中,四边形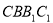 为矩形,
为矩形,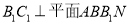 ,四边形
,四边形 为梯形,
为梯形,
且 ,
,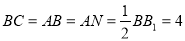 .
.

(1)求证: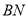
 ;
;
(2)求此五面体的体积.
(1)详见解析 ;(2)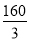
【解析】
试题分析:(1)要证明直线和平面垂直,只需证明直线和平面内的两条相交直线垂直,本题因为 面
面
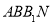 ,则
,则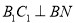 ,故只需证明
,故只需证明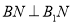 ,在
,在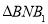 中,易求个边长度,故利用勾股定理证明
中,易求个边长度,故利用勾股定理证明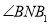 是直角,进而证明
是直角,进而证明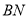
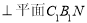 ;(2)求几何体体积,若是规则几何体,直接利用体积公式计算,若是不规则几何体,可采取割补的方法.本题中五面体的体积可分割为
;(2)求几何体体积,若是规则几何体,直接利用体积公式计算,若是不规则几何体,可采取割补的方法.本题中五面体的体积可分割为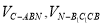 两部分体积来求.
两部分体积来求.
试题解析:(1)证明:连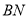 ,过
,过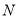 作
作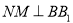 ,垂足为
,垂足为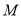 ,
,
∵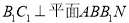 ,
,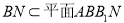 ,
,
∴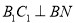 , 2分
, 2分
又,BC=4,AB=4,BM=AN=4,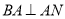 ,
,
∴ 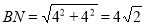 ,
,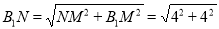 =
=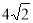 ,
,
∵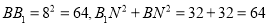 ,
,
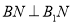 , 4分
, 4分
∵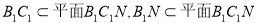 ,
,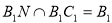

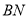
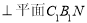 6分
6分
(2)连接CN, , 8分
, 8分
又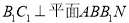 ,所以平面
,所以平面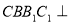 平面
平面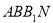 ,且平面
,且平面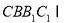
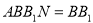 ,
,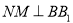 ,
,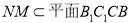 ,
,
∴ 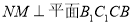 , 9分
, 9分
 11分
11分
此几何体的体积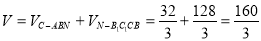 12分
12分
考点:1、直线与平面垂直;2、几何体体积.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考文科数学试卷(解析版) 题型:解答题
已知函数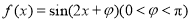 的图像经过点
的图像经过点 .
.
(1)求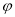 的值;
的值;
(2)在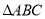 中,
中, 、
、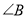 、
、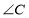 所对的边分别为
所对的边分别为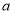 、
、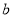 、
、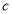 ,若
,若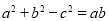 ,且
,且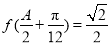 .求
.求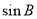 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考理科数学试卷(解析版) 题型:解答题
已知直线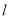 :
: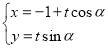 (
(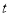 为参数,?为
为参数,?为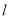 的倾斜角),以坐标原点为极点,
的倾斜角),以坐标原点为极点,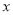 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线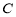 为:
为: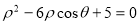 .
.
(1)若直线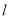 与曲线
与曲线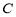 相切,求
相切,求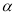 的值;
的值;
(2)设曲线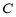 上任意一点的直角坐标为
上任意一点的直角坐标为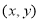 ,求
,求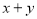 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考理科数学试卷(解析版) 题型:选择题
三棱锥的三视图如图,正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积为 ( )
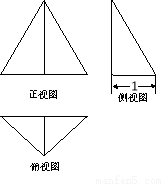
A.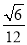 B.
B.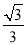 C.
C.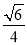 D.
D.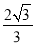
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考文科数学试卷(解析版) 题型:解答题
已知直线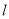 :
: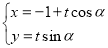 (
(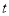 为参数,?为
为参数,?为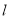 的倾斜角),以坐标原点为极点,
的倾斜角),以坐标原点为极点,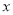 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线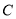 为:
为: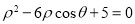 .
.
(1)若直线 与曲线
与曲线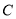 相切,求
相切,求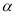 的值;
的值;
(2)设曲线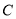 上任意一点的直角坐标为
上任意一点的直角坐标为 ,求
,求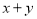 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考文科数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.命题“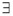 x0∈R,x02+x0+1<0”的否定是:“
x0∈R,x02+x0+1<0”的否定是:“ x∈R,x2+x+1>0”;
x∈R,x2+x+1>0”;
B.“x=-1”是“x2-5x-6=0”的必要不充分条件;
C.命题“若x2=1,则x=1”的否命题是:若x2=1,则x≠1;
D.命题“若x=y,则sin x=sin y”的逆否命题为真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com