
| A. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=0 | B. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=-1 | C. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{3}{4}$ | D. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{2}{3}$ |
分析 由题意可知三向量起点在圆上,终点组成边长为1的等边三角形,建立坐标系,设起点坐标,表示出各向量的数量积,利用三角恒等变换求出最值即可得出结论.
解答 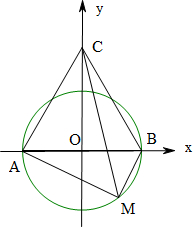 解:设$\overrightarrow{MA}=\overrightarrow{{a}_{1}}$,$\overrightarrow{MB}=\overrightarrow{{a}_{2}}$,$\overrightarrow{MC}$=$\overrightarrow{{a}_{3}}$,
解:设$\overrightarrow{MA}=\overrightarrow{{a}_{1}}$,$\overrightarrow{MB}=\overrightarrow{{a}_{2}}$,$\overrightarrow{MC}$=$\overrightarrow{{a}_{3}}$,
∵|$\overrightarrow{{a}_{i}}$-$\overrightarrow{{a}_{i+1}}$|=1,∴△ABC是边长为1的等边三角形,
∵$\overrightarrow{{a}_{1}}⊥\overrightarrow{{a}_{2}}$,∴M在以AB为直径的圆上,
以AB为x轴,以AB的中垂线为y轴建立平面坐标系,则A(-$\frac{1}{2}$,0),B($\frac{1}{2}$,0),C(0,$\frac{\sqrt{3}}{2}$),
设M($\frac{1}{2}$cosα,$\frac{1}{2}$sinα),
则$\overrightarrow{MA}$=(-$\frac{1}{2}$-$\frac{1}{2}$cosα,-$\frac{1}{2}$sinα),$\overrightarrow{MB}$=($\frac{1}{2}-\frac{1}{2}$cosα,-$\frac{1}{2}$sinα),$\overrightarrow{MC}$=(-$\frac{1}{2}$cosα,$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$sinα),
∴$\overrightarrow{MA}•\overrightarrow{MC}$=$\frac{1}{2}$cosα($\frac{1}{2}$+$\frac{1}{2}$cosα)+$\frac{1}{2}$sinα($\frac{1}{2}$sinα-$\frac{\sqrt{3}}{2}$)=$\frac{1}{4}$+$\frac{1}{2}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα)=$\frac{1}{4}$+$\frac{1}{2}$cos(α+$\frac{π}{3}$),
∴$\overrightarrow{MA}•\overrightarrow{MC}$的最大值为$\frac{1}{4}+\frac{1}{2}$=$\frac{3}{4}$,最小值为$\frac{1}{4}$-$\frac{1}{2}$=-$\frac{1}{4}$.
由图形的对称性可知$\overrightarrow{MB}•\overrightarrow{MC}$的最大值为$\frac{3}{4}$,最小值为-$\frac{1}{4}$.
又$\overrightarrow{MA}•\overrightarrow{MB}$=0,
∴($\overrightarrow{{a}_{i}}•\overrightarrow{{a}_{i+1}}$)max=$\frac{3}{4}$,($\overrightarrow{{a}_{i}}•\overrightarrow{{a}_{i+1}}$)min=-$\frac{1}{4}$.
故选:C.
点评 本题考查了平面向量的数量积运算,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{6}{7}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $\frac{\sqrt{7}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
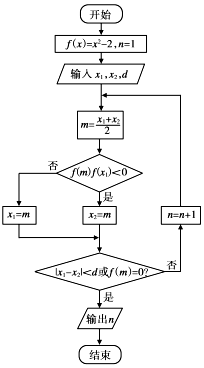 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{6}$ | B. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{12}$ | ||
| C. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{12}$ | D. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com