
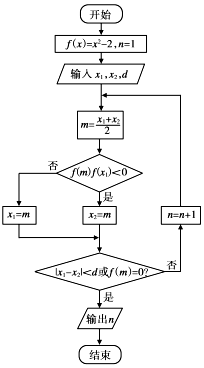
 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 按照用二分法求函数零点近似值得步骤求解即可.注意验证精确度的要求.
解答 解:模拟执行程序框图,可得
x1=1,x2=2,d=0.01,m=$\frac{3}{2}$,n=1
满足条件:f(1)•f($\frac{3}{2}$)<0,x2=$\frac{3}{2}$,
不满足条件:|x1-x2|<0.01,m=$\frac{5}{4}$,n=2,不满足条件:f(1)•f($\frac{5}{4}$)<0,x1=$\frac{5}{4}$,
不满足条件:|x1-x2|<0.01,m=$\frac{11}{8}$,n=3,不满足条件:f($\frac{5}{4}$)•f($\frac{11}{8}$)<0,x1=$\frac{11}{8}$,
不满足条件:|x1-x2|<0.01,m=$\frac{23}{16}$,n=4,不满足条件:f($\frac{11}{8}$)•f($\frac{23}{16}$)<0,x1=$\frac{23}{16}$,
不满足条件:|x1-x2|<0.01,m=$\frac{47}{32}$,n=5,不满足条件:f($\frac{23}{16}$)•f($\frac{47}{32}$)<0,x1=$\frac{47}{32}$,
不满足条件:|x1-x2|<0.01,m=$\frac{95}{64}$,n=6,不满足条件:f($\frac{47}{32}$)•f($\frac{95}{64}$)<0,x1=$\frac{95}{64}$,
不满足条件:|x1-x2|<0.01,m=$\frac{191}{128}$,n=7,不满足条件:f($\frac{95}{64}$)•f($\frac{191}{128}$)<0,x1=$\frac{191}{128}$,
满足条件:|x1-x2|<0.01,退出循环,输出n的值为7.
故选:B.
点评 本题主要考查用二分法求区间根的问题,属于基础题型.二分法是把函数的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而求零点近似值的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=0 | B. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=-1 | C. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{3}{4}$ | D. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
在圆 内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A.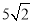 B.
B.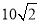 C.
C.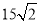 D.
D.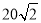
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com