
分析 (1)求出圆的半径,即可求圆O的方程;
(2)分类讨论,利用圆心到直线的距离等于半径,即可求切线的方程.
解答 解:(1)圆心到直线的距离d=$\frac{4}{\sqrt{1+3}}$=2,
∴求圆O的方程为x2+y2=4;
(2)斜率不存在时,x=2满足题意;
斜率存在时,设直线方程为y-3=k(x-2),即kx-y-2k+3=0,
圆心到直线的距离d=$\frac{|-2k+3|}{\sqrt{{k}^{2}+1}}$=2,∴k=$\frac{5}{12}$,切线的方程为5x-12y+26=0.
综上所述切线的方程为x=2或5x-12y+26=0.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 9 | 14 | 14 | 13 | 12 | x | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | e | C. | -$\frac{1}{e}$ | D. | -e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-3,1) | C. | (-1,-3 ) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 35 | C. | 30 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
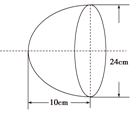 如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )
如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )| A. | 10 cm | B. | 7.2 cm | C. | 2.4 cm | D. | 3.6 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com