
分析 (Ⅰ)由题意设出椭圆标准方程,且求得c,a的值,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)(1)写出直线方程,与椭圆方程联立,利用判别式大于0求得k的范围;
(2)利用根与系数的关系求出P,Q两点的横坐标与纵坐标的和,结合$\overrightarrow{OP}$+$\overrightarrow{OQ}$与$\overrightarrow{AB}$共线求得k值,与(1)中求出的k的范围矛盾.
解答 解:(Ⅰ)由已知可得椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
且2c=2,$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$,∴c=1,a=$\sqrt{2}$,b2=a2-c2=1,
∴椭圆方程为:$\frac{x^2}{2}+{y^2}=1$;
( II)①由已知条件,直线l的方程为$y=kx+\sqrt{2}$,
代入椭圆方程得$\frac{x^2}{2}+{(kx+\sqrt{2})^2}=1$.
整理得$({\frac{1}{2}+{k^2}}){x^2}+2\sqrt{2}kx+1=0$,①
直线l与椭圆有两个不同的交点P和Q等价于$△=8{k^2}-4({\frac{1}{2}+{k^2}})=4{k^2}-2>0$,
解得$k<-\frac{{\sqrt{2}}}{2}$或$k>\frac{{\sqrt{2}}}{2}$.
即k的取值范围为$({-∞,-\frac{{\sqrt{2}}}{2}})∪({\frac{{\sqrt{2}}}{2},+∞})$;
②设P(x1,y1),Q(x2,y2),
则$\overrightarrow{OP}+\overrightarrow{OQ}=({x_1}+{x_2},{y_1}+{y_2})$,
由方程①,得${x_1}+{x_2}=-\frac{{4\sqrt{2}k}}{{1+2{k^2}}}$.②
又${y_1}+{y_2}=k({x_1}+{x_2})+2\sqrt{2}$.③
而$A(\sqrt{2},0),B(0,1),\overrightarrow{AB}=(-\sqrt{2},1)$.
∴$\overrightarrow{OP}+\overrightarrow{OQ}$与$\overrightarrow{AB}$共线等价于${x_1}+{x_2}=-\sqrt{2}({y_1}+{y_2})$,
将②③代入上式,解得$k=\frac{{\sqrt{2}}}{2}$.
由(Ⅰ)知$k<-\frac{{\sqrt{2}}}{2}$或$k>\frac{{\sqrt{2}}}{2}$,
故没有符合题意的常数k.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了向量法在求解圆锥曲线问题中的应用,是中档题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(-1,+∞)上是增函数 | B. | 在(-1,+∞)上是减函数 | ||
| C. | 在(-∞,1)上是增函数 | D. | 在(-∞,1)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=lgx2,g(x)=2lgx | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x-1}$,g(x)=$\sqrt{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
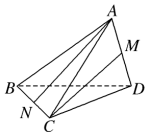 如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是( )
如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是( )| A. | $\frac{7}{8}$ | B. | -$\frac{7}{8}$ | C. | -$\frac{7}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(2)<f(4) | B. | f(2)<f(1)<f(4) | C. | f(4)<f(2)<f(1) | D. | f(4)<f(1)<f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [0,2] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com