
| A. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=lgx2,g(x)=2lgx | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x-1}$,g(x)=$\sqrt{x+1}$ |
分析 要表示同一个函数,必须有相同的对应法则,相同的定义域,观察四个选项,得到有一组函数的对应法则不同,有两组函数的定义域不同,只有A选项,整理以后完全相同.
解答 解:A,f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$=|x|,定义域和对应关系相同是同一函数;
B,f(x)=lgx2,(x≠0),g(x)=2lgx,(x>0),定义域不同,不为同一函数;
C,f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1定义域不同,不为同一函数;
D,f(x)=$\sqrt{x-1}$,g(x)=$\sqrt{x+1}$对应关系不同,不为同一函数.
故选A.
点评 本题考查判断两个函数是否为同一个函数,这种题目一般从三个方面来观察,绝大部分题目是定义域不同,有一小部分是对应法则不同,只有极个别的是值域不同.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | e | C. | -$\frac{1}{e}$ | D. | -e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
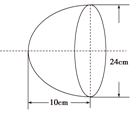 如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )
如图所示,汽车前反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处,已知灯口的直径是24cm,灯深10cm.那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )| A. | 10 cm | B. | 7.2 cm | C. | 2.4 cm | D. | 3.6 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $(-\sqrt{2},\sqrt{2})$ | C. | (-1,1) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,0) | D. | (-$\frac{2}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com