
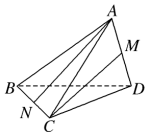
 如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是( )
如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是( )| A. | $\frac{7}{8}$ | B. | -$\frac{7}{8}$ | C. | -$\frac{7}{25}$ | D. | $\frac{7}{25}$ |
分析 利用中位线作出异面直线所成的角,然后在三角形中利用余弦定理求出余弦值即可.
连结ND,取ND 的中点为E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC.
解答 解:由题意:三棱锥ABCD中,连结ND,取ND 的中点为E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC.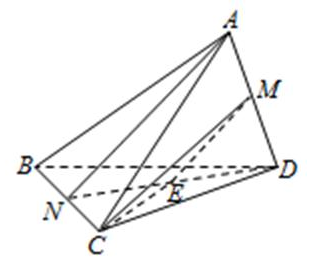
∵AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,
∴AN=$2\sqrt{2}$,ME=EN=$\sqrt{2}$,MC=2$\sqrt{2}$,
又∵EN⊥NC,∴EC=$\sqrt{N{C}^{2}+N{E}^{2}}$=$\sqrt{3}$;
cos∠EMC=$\frac{M{C}^{2}+M{E}^{2}-E{C}^{2}}{2MC•ME}$=$\frac{2+8-3}{2×\sqrt{2}×2\sqrt{2}}$=$\frac{7}{8}$.
∴异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.
故选A.
点评 本题考查了异面直线所成的角,余弦定理的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-3,1) | C. | (-1,-3 ) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{x}$-x | B. | f(x)=x3 | C. | f(x)=ln x | D. | f(x)=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | 工人数(人) |
| 19 | 1 |
| 28 | 3 |
| 29 | 3 |
| 30 | 5 |
| 31 | 4 |
| 32 | 3 |
| 40 | 1 |
| 合计 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com