
分析 由正四面体的棱长为a,所以此四面体一定可以放在棱长为$\frac{\sqrt{2}}{2}a$的正方体中,所以此四面体的外接球即为此正方体的外接球,由此能求出此四面体的外接球的半径,再代入面积公式、体积公式计算.
解答 解:∵正四面体的棱长为a,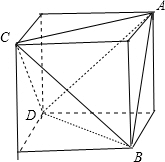
∴此四面体一定可以放在正方体中,
∴我们可以在正方体中寻找此四面体.
如图所示,四面体ABCD满足题意,BC=a,
∴正方体的棱长为$\frac{\sqrt{2}}{2}$a,
∴此四面体的外接球即为此正方体的外接球,
∵外接球的直径=正方体的对角线长,
∴外接球的半径为R=$\frac{1}{2}×\sqrt{\frac{1}{2}+\frac{1}{2}+\frac{1}{2}}$a=$\frac{\sqrt{6}}{4}$a.
点评 此题看成正方体截得的正四面体,则此正四面体的外接球半径即是正四面体的外接球半径是关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 94 | B. | 98 | C. | 99 | D. | 104 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知E,F分别为正方体ABCD-A1B1C1D1的棱AA1和CC1上的点,且$\frac{AE}{A{A}_{1}}$=$\frac{{C}_{1}F}{C{C}_{1}}$=λ,λ∈(0,1),延长D1E,D1F与平面ABCD分别相交于M,N两点.
如图,已知E,F分别为正方体ABCD-A1B1C1D1的棱AA1和CC1上的点,且$\frac{AE}{A{A}_{1}}$=$\frac{{C}_{1}F}{C{C}_{1}}$=λ,λ∈(0,1),延长D1E,D1F与平面ABCD分别相交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 2 | 4 | 7 | 5 | 1 | 8 |
| A. | 4054 | B. | 5046 | C. | 5075 | D. | 6043 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com