Question

【题目】设是定义在上的函数，若存在，使得在单调递增，在上单调递减，则称为上的单峰函数，为峰点，包含峰点的区间称为含峰区间，其含峰区间的长度为：．

（1）判断下列函数中，哪些是“上的单峰函数”？若是，指出峰点；若不是，说出原因；；

（2）若函数是上的单峰函数，求实数的取值范围；

（3）若函数是区间上的单峰函数，证明：对于任意的，若，则为含峰区间；若，则为含峰区间；试问当满足何种条件时，所确定的含峰区间的长度不大于0.6．

Answer 1

【答案】（1）见解析（2）（3）证明见解析；

【解析】

（1）画出四个函数图像，根据图像集合单峰函数的定义进行判断.

（2）利用的导函数的零点在区间列不等式，解不等式求得的取值范围.

（3）分成、两种情况进行分类讨论，利用反证法证得结论成立.根据含峰区间的长度的概念列不等式，由此确定满足的条件.

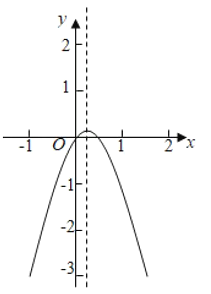
（1）①图像如下图所示，其对称轴为，由图可知，是上的单峰函数，峰点为；

②的图像如下图所示，其对称轴为，由图可知，是上的单峰函数，峰点为；

③的图像如下图所示，根据图像可知，不是上的单峰函数；

④的图像如下图所示，其对称轴为，由图可知，是上的单峰函数，峰点为.

（2）函数是上的单峰函数，令，解得，故时，递增，时，递减，所以，解得，故的取值范围是.

（3）设为的峰点，则由单峰函数定义可知，在上递增，在上递减.

当时，假设，则，从而，与矛盾，所以，即是含峰区间.

当时，假设，则，从而，与矛盾，所以，即是含峰区间.

在所得的含峰区间内选取，由与或与，确定一个新的含峰区间，对先选择的，，①，在第一次确定的含峰区间为的情况下，的取值应满足②，由①②可得，当时，含峰区间的长度为.

由条件，得，从而.因此确定的含峰区间的长度不大于，只要取.