
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,得到函数f(x)的最小值g(t),根据函数的单调性求出g(t)的最大值即可;
(3)求出h(x)的导数,根据函数的单调性求出h(x)的最小值即可.
解答 解:(1)t=1时,f(x)=$\frac{2}{x}$+lnx,(x>0),
f′(x)=$\frac{x-2}{{x}^{2}}$,∵x∈(0,+∞),
故f(x)在(0,2)递减,在(2,+∞)递增;
(2)当t>0时,f′(x)=$\frac{tx-2}{{x}^{2}}$=0⇒x=$\frac{2}{t}$,
x,f′(x),f(x)的变化如下:
| x | (0,$\frac{2}{t}$) | $\frac{2}{t}$ | ($\frac{2}{t}$,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
| t | (0,2) | 2 | (2,+∞) |
| g'(t) | + | 0 | - |
| g(t) | ↗ | 极大值 | ↘ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $18\sqrt{2}$ | B. | $36\sqrt{2}$ | C. | 18 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
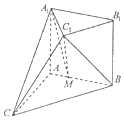 如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.
如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据,则其线性回归直线方程是______________
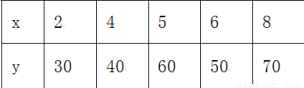
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:解答题
某村计划建造一个室内面积为800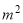 的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1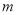 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3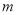 宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大,最大种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com