练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
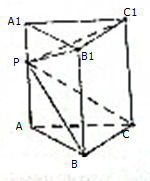
    如图所示，点P为三棱柱ABC-A1B1C1侧棱AA1上一动点，若四棱锥P-BCC1B1的体积为V，则三棱柱ABC-A1B1C1的体积为（　　）
    A、2V
    B、3V
    C、
    4V
    3
    D、
    3V
    2
    考点：棱柱、棱锥、棱台的体积
    专题：空间位置关系与距离
    分析：利用AA1到对面距离不变，转化P到A点，利用棱锥与棱柱的体积关系，即可得出结论．
    解答： 解：由题意，借款合同是棱柱，所以AA1到对面距离不变，移动P到A点，由棱锥的体积的推导方法可知：
    VP-BCC1B1=
    2
    3
    VABC-A1B1C1．∴VABC-A1B1C1=
    3
    2
    V    ．
    故选：D．
    点评：本题考查棱柱、棱锥、棱台的体积，考查学生的计算能力，基本知识的考查．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1+a2=4，a2+a3=8，则a7等于（　　）
    A、7B、10C、13D、19

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知角θ的终边上有一点P（x，-1）（x≠0），且tanθ=-x，求sinθ，cosθ；
    （2）已知函数f（x）=
    1-sin(x-
    3π
    2
    )+cos(x+
    π
    2
    )+tan
    3
    4
    π
    cosx
    ，设tanα=-
    4
    3
    ，求f（α）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A={x∈N|1≤x＜6}，则下列正确的是（　　）
    A、6∈AB、0∈A
    C、3?AD、3.5∉a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=2cos（
    1
    2
    x-
    π
    3
    ），x∈[-π，π]．
    （1）求函数的单调区间；
    （2）求函数的最小值及取得最小值时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

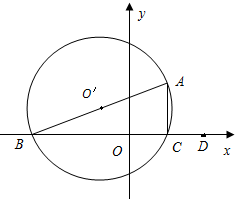    如图，在平面直角坐标系中，△ABC内接于⊙O，其中AB为⊙O直径，A（1，3），B（-3，0），C（1，0）．
    （1）请在x轴上找一点D，使得△BDA与△BAC相似（不包含全等），并求出点D的坐标；
    （2）在（1）的条件下，如果P，Q分别是BA，BD上的动点，连接PQ，设BP=DQ=m．问是否存在这样的m，使得△BPQ与△BDA相似？若存在，求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC中，角A、B、C所对应的边分别为a，b，c，若
    a-c
    sinB-sinC
    =
    b
    sinA+sinB

    （1）求角A；
    （2）若函数f（x）=cos2（x+A）-sin2（x-A）+
    1
    2
    cosx，x∈[A，π]    ，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

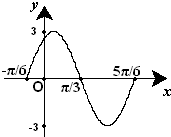    已知函数f（x）=Asin（ωx+φ） （A＞0，ω＞0，|φ|＜π）的一段图象（如图）所示．
    （1）求函数的解析式；
    （2）写出这个函数的单调增区间；
    （3）若x∈[-
    π
    6
    ，
    π
    3
    ]时，函数g（x）=f（x）+m的最小值为2，试求出函数g（x）的最大值并求出此时x的取值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线y2=-8x的焦点为F1，准线与x轴的交点为F2，直线l：x-y+4=0，以F1、F2为焦点的椭圆C过直线l上一点．
    （1）求长轴最短时椭圆C的方程；
    （2）在（1）中的椭圆上存在四点M、N、P、Q满足：
    PF2
    ∥
    F2Q
    ，
    MF2
    ∥
    F2N
    ，
    PF2
    ⊥
    F2M
    ，求四边形PMQN的面积的最大值和最小值．

    查看答案和解析>>

    同步练习册答案