
设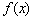 是定义在
是定义在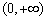 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记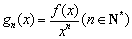 .若对定义域内的每一个
.若对定义域内的每一个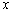 ,总有
,总有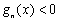 ,则称
,则称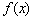 为“
为“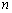 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个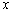 ,总有
,总有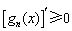 ,则称
,则称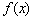 为“
为“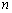 阶不减函数”(
阶不减函数”(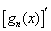 为函数
为函数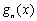 的导函数).
的导函数).
(1)若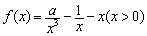 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数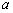 的取值范围;
的取值范围;
(2)对任给的“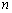 阶不减函数”
阶不减函数”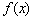 ,如果存在常数
,如果存在常数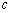 ,使得
,使得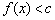 恒成立,试判断
恒成立,试判断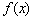 是否为“
是否为“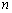 阶负函数”?并说明理由.
阶负函数”?并说明理由.
科目:高中数学 来源: 题型:
若奇函数f(x)在(0,+∞)上是增函数,又f(-3)=0,则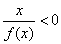 的解集为( )
的解集为( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
以下说法,正确的个数为:( )
①公安人员由罪犯的脚印的尺寸估计罪犯的身高情况,所运用的是类比推理.
②农谚“瑞雪兆丰年”是通过归纳推理得到的.
③由平面几何中圆的一些性质,推测出球的某些性质这是运用的类比推理.
④个位是5的整数是5的倍数,2375的个位是5,因此2375是5的倍数,这是运用的演绎推理.
A.0 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com