
分析 确定f(x)与g(x)的图象交点的横坐标的范围,作出函数h(x)的图象,即可得到结论.
解答 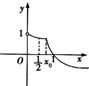 解:记f(x)与g(x)的图象交点的横坐标为x=x0,
解:记f(x)与g(x)的图象交点的横坐标为x=x0,
∴f($\frac{1}{2}$)=$\frac{\sqrt{2}}{2}$<1=log${\;}_{\frac{1}{2}}$$\frac{1}{2}$=g($\frac{1}{2}$),
∴x0∈($\frac{1}{2}$,1).
由于f(x)与g(x)均为减函数,
∴h(x)为减函数,
∵h(x)≥$\frac{1}{2}$,
∴$\frac{1}{2}$x≥$\frac{1}{2}$=($\frac{1}{2}$)1,
∴x<1,
∵log${\;}_{\frac{1}{2}}$x≥$\frac{1}{2}$=$\frac{1}{2}$log${\;}_{\frac{1}{2}}$$\frac{1}{2}$=log${\;}_{\frac{1}{2}}$$\frac{\sqrt{2}}{2}$,
∴0<x≤$\frac{\sqrt{2}}{2}$,
综上所述不等式的解集为(0,$\frac{\sqrt{2}}{2}$],
故答案为:(0,$\frac{\sqrt{2}}{2}$]
点评 本题考查新定义,考查不等式的解法,考查数形结合的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\lim_{n→∞}a_n^2={A^2}$,则$\underset{lim}{n→∞}$an=A | B. | 若an>0,$\lim_{n→∞}{a_n}=A$,则A>0 | ||
| C. | 若$\lim_{n→∞}{a_n}=A$,则$\lim_{n→∞}a_n^2={A^2}$ | D. | 若$\underset{lim}{n→∞}$an=A,则$\lim_{n→∞}na_n^{\;}=n{A^{\;}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{x{\;}^{2}-x,x≤1}\\{x-3,x>1}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{x{\;}^{2}-x,x≤1}\\{x-3,x>1}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
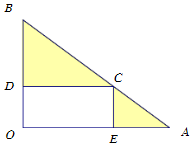 某公园有一个直角三角形地块,现计划把它改造成一块矩形和两块三角形区域.如图,矩形区域用于娱乐城设施的建设,三角形BCD区域用于种植甲种观赏花卉,三角形CAE区域用于种植乙种观赏花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲种花卉每平方千米造价1万元,乙种花卉每平方千米造价4万元,设OE=x千米.试建立种植花卉的总造价为y(单位:万元)关于x的函数关系式;求x为何值时,种植花卉的总造价最小,并求出总造价.
某公园有一个直角三角形地块,现计划把它改造成一块矩形和两块三角形区域.如图,矩形区域用于娱乐城设施的建设,三角形BCD区域用于种植甲种观赏花卉,三角形CAE区域用于种植乙种观赏花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲种花卉每平方千米造价1万元,乙种花卉每平方千米造价4万元,设OE=x千米.试建立种植花卉的总造价为y(单位:万元)关于x的函数关系式;求x为何值时,种植花卉的总造价最小,并求出总造价.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com