
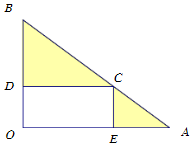
 某公园有一个直角三角形地块,现计划把它改造成一块矩形和两块三角形区域.如图,矩形区域用于娱乐城设施的建设,三角形BCD区域用于种植甲种观赏花卉,三角形CAE区域用于种植乙种观赏花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲种花卉每平方千米造价1万元,乙种花卉每平方千米造价4万元,设OE=x千米.试建立种植花卉的总造价为y(单位:万元)关于x的函数关系式;求x为何值时,种植花卉的总造价最小,并求出总造价.
某公园有一个直角三角形地块,现计划把它改造成一块矩形和两块三角形区域.如图,矩形区域用于娱乐城设施的建设,三角形BCD区域用于种植甲种观赏花卉,三角形CAE区域用于种植乙种观赏花卉.已知OA=4千米,OB=3千米,∠AOB=90°,甲种花卉每平方千米造价1万元,乙种花卉每平方千米造价4万元,设OE=x千米.试建立种植花卉的总造价为y(单位:万元)关于x的函数关系式;求x为何值时,种植花卉的总造价最小,并求出总造价. 分析 求出三角形BCD、三角形CAE区域的面积,可得函数解析式,利用配方法,可得函数的最值.
解答 解:由题意,CD=OE=x.由△BCD∽△BAO知BD=$\frac{3}{4}$x,所以S△BCD=$\frac{3}{8}$x2.
同理得S△CAE=$\frac{3}{8}$(x-4)2.…6分
所以,y=$\frac{3}{8}$[x2+(x-4)2×4]=$\frac{3}{8}$(5x2-32x+64),其中,0<x<4.…10分
y=$\frac{3}{8}$[5(x-$\frac{16}{5}$)2+$\frac{64}{5}$]…13分
因为0<<4,…14分
所以x=$\frac{16}{5}$时,y有最小值为4.8万元.…15分
答:x为$\frac{16}{5}$时,种植花卉的总造价最小,总造价最小值为4.8万元.
点评 本题考查利用数学知识解决实际问题,考查配方法的运用,确定函数的解析式是关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,$\sqrt{2}$) | C. | (1,2) | D. | (0,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P-AC-B的大小为60°;
如图,在三棱锥P-ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P-AC-B的大小为60°;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com