若直线过点且倾斜角为30°.则该直线的方程为y=$\frac{{\sqrt{3}}}{3}$x-4．题目和参考答案——青夏教育精英家教网—

7．若直线过点（$\sqrt{3}$，-3）且倾斜角为30°，则该直线的方程为y=$\frac{{\sqrt{3}}}{3}$x-4．

分析由直线的倾斜角求出直线的斜率，代入直线方程的点斜式得答案．

解答解：∵直线的倾斜角为30°，∴其斜率为tan30°=$\frac{\sqrt{3}}{3}$，
由直线过点（$\sqrt{3}$，-3），
∴直线方程为y-3=$\frac{\sqrt{3}}{3}（x-\sqrt{3}）$，即y=$\frac{{\sqrt{3}}}{3}$x-4．
故答案为：y=$\frac{{\sqrt{3}}}{3}$x-4．

点评本题考查待定系数法求直线方程，考查了直线方程的点斜式，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

17．已知集合M={x|$\frac{x}{x-1}$≥0，x∈R}，N={y|y=3x²+1，x∈R}，则M∩N为（　　）

A．

{x|x＞1}

B．

{x|x≥1}

C．

{x＞1或x≤0}

D．

{x|0≤x≤1}

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．函数f（x）=x²+2x-3，x∈[-2，1]，函数f（x）的值域为[-4，0]．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．

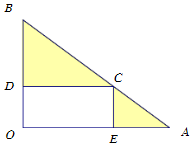某公园有一个直角三角形地块，现计划把它改造成一块矩形和两块三角形区域．如图，矩形区域用于娱乐城设施的建设，三角形BCD区域用于种植甲种观赏花卉，三角形CAE区域用于种植乙种观赏花卉．已知OA=4千米，OB=3千米，∠AOB=90°，甲种花卉每平方千米造价1万元，乙种花卉每平方千米造价4万元，设OE=x千米．试建立种植花卉的总造价为y（单位：万元）关于x的函数关系式；求x为何值时，种植花卉的总造价最小，并求出总造价．