
分析 (Ⅰ)由导数与极值的关系知可转化为方程f′(x)=lnx-ax=0在(0,+∞)有两个不同根;再转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,或转化为函数g(x)=$\frac{lnx}{x}$与函数y=a的图象在(0,+∞)上有两个不同交点;或转化为g(x)=lnx-ax有两个不同零点,从而讨论求解;
(Ⅱ)问题等价于ln$\frac{{x}_{1}}{{x}_{2}}$>$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$,令$\frac{x_1}{x_2}=t$,则t>1,$ln\frac{x_1}{x_2}>\frac{{2({{x_1}-{x_2}})}}{{{x_1}+{x_2}}}?lnt>\frac{{2({t-1})}}{t+1}$,设$g(t)=lnt-\frac{{2({t-1})}}{t+1},t>1$,根据函数的单调性证出结论即可.
解答 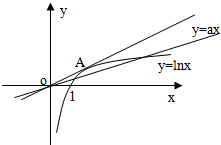 解:(Ⅰ)由题意知,函数f(x)的定义域为(0,+∞),
解:(Ⅰ)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根;
即方程lnx-ax=0在(0,+∞)有两个不同根;
(解法一)转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如右图.
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0=$\frac{1}{{x}_{0}}$,又k=$\frac{l{nx}_{0}}{{x}_{0}}$,
故 $\frac{1}{{x}_{0}}$=$\frac{l{nx}_{0}}{{x}_{0}}$,
解得,x0=e,
故k=$\frac{1}{e}$,
故0<a<$\frac{1}{e}$.
(解法二)转化为函数g(x)=$\frac{lnx}{x}$与函数y=a的图象在(0,+∞)上有两个不同交点.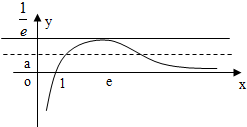
又g′(x)=$\frac{1-lnx}{{x}^{2}}$,
即0<x<e时,g′(x)>0,x>e时,g′(x)<0,
故g(x)在(0,e)上单调增,在(e,+∞)上单调减.
故g(x)极大=g(e)=$\frac{1}{e}$;
又g(x)有且只有一个零点是1,且在x→0时,g(x)→-∞,在在x→+∞时,g(x)→0,
故g(x)的草图如右图,
可见,要想函数g(x)=$\frac{lnx}{x}$与函数y=a的图象在(0,+∞)上有两个不同交点,
只须0<a<$\frac{1}{e}$.
(解法三)令g(x)=lnx-ax,从而转化为函数g(x)有两个不同零点,
而g′(x)=$\frac{1}{x}$-ax=$\frac{1-ax}{x}$(x>0),
若a≤0,可见g′(x)>0在(0,+∞)上恒成立,所以g(x)在(0,+∞)单调增,
此时g(x)不可能有两个不同零点.
若a>0,在0<x<$\frac{1}{a}$时,g′(x)>0,在x>$\frac{1}{a}$时,g′(x)<0,
所以g(x)在(0,$\frac{1}{a}$)上单调增,在($\frac{1}{a}$,+∞)上单调减,从而g(x)极大=g($\frac{1}{a}$)=ln$\frac{1}{a}$-1,
又因为在x→0时,g(x)→-∞,在在x→+∞时,g(x)→-∞,
于是只须:g(x)极大>0,即ln$\frac{1}{a}$-1>0,所以0<a<$\frac{1}{e}$.
综上所述,0<a<$\frac{1}{e}$.
(Ⅱ)由(Ⅰ)可知x1,x2分别是方程lnx-ax=0的两个根,
即lnx1=ax1,lnx2=ax2,
设x1>x2,作差得ln$\frac{{x}_{1}}{{x}_{2}}$=a(x1-x2),即a=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{{x}_{1}-x}_{2}}$
原不等式${x_1}•{x_2}>{e^2}$等价于ln$\frac{{x}_{1}}{{x}_{2}}$>$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$,
令$\frac{x_1}{x_2}=t$,则t>1,$ln\frac{x_1}{x_2}>\frac{{2({{x_1}-{x_2}})}}{{{x_1}+{x_2}}}?lnt>\frac{{2({t-1})}}{t+1}$,
设$g(t)=lnt-\frac{{2({t-1})}}{t+1},t>1$,$g'(t)=\frac{{{{({t-1})}^2}}}{{t{{({t+1})}^2}}}>0$,
∴函数g(t)在(1,+∞)上单调递增,
∴g(t)>g(1)=0,
即不等式$lnt>\frac{{2({t-1})}}{t+1}$成立,
故所证不等式${x_1}•{x_2}>{e^2}$成立.
点评 本题考查了导数的综合应用及分类讨论,转化思想,数形结合的思想方法的应用,属于综合题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,3) | B. | (-3,4) | C. | (0,3) | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {1} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,4) | C. | [2,4) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com