
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
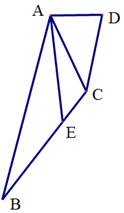 在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
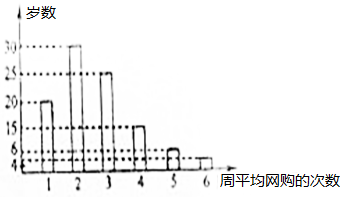 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
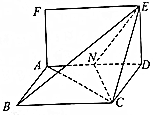 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com