
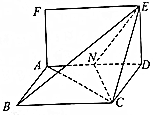
 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.分析 (Ⅰ) 作FE的中点P,连接CP交BE于点M,M点即为所求的点,由PE∥AD,AD∥BC,得PE∥BC,$\frac{BM}{ME}=\frac{BC}{PE}=2$,
(Ⅱ)由(Ⅰ)得PN⊥ND,PN⊥NC,以N为空间坐标原点,NC,ND,NP分别为x,y,z轴建立空间直角坐标系N-xyz,N(0,0,0),C($\sqrt{3}$,0,0),D(0,1,0),E(0,1,1),利用向量法求解.
解答 解:(Ⅰ) 作FE的中点P,连接CP交BE于点M,M点即为所求的点.…(2分)
证明:连接PN,∵N是AD的中点,P是FE的中点,∴PN∥AF,
又PN?平面MNC,AF?平面MNC,
∴直线AF∥平面MNC.
…(5分)
∵PE∥AD,AD∥BC,∴PE∥BC,
∴$\frac{BM}{ME}=\frac{BC}{PE}=2$.…(6分)
(Ⅱ)由(Ⅰ)知PN⊥AD,又面ADEF⊥面ABCD,面ADEF∩面ABCD=AD,PN?面ADEF,
所以PN⊥面ABCD. …(8分)
故PN⊥ND,PN⊥NC.…(9分)
以N为空间坐标原点,NC,ND,NP分别为x,y,z轴建立空间直角坐标系N-xyz,
∵∠ADC=$\frac{π}{3}$,AD=DC=2,∴△ADC为正三角形,NC=$\sqrt{3}$,
∴N(0,0,0),C($\sqrt{3}$,0,0),D(0,1,0),E(0,1,1),
∴$\overrightarrow{NE}$=(0,1,1),$\overrightarrow{NC}$=($\sqrt{3}$,0,0),$\overrightarrow{DE}$=(0,0,1),$\overrightarrow{DC}$=($\sqrt{3}$,-1,0),
设平面NEC的一个法向量n1=(x,y,z),则由n1•$\overrightarrow{NE}$=0,n1•$\overrightarrow{NC}$=0可得
$\left\{\begin{array}{l}{y+z=0}\\{\sqrt{3}x=0}\end{array}\right.$令y=1,则n1=(0,1,-1).
设平面CDE的一个法向量n2=(x1,y1,z1),则由n2•$\overrightarrow{DE}$=0,n2•$\overrightarrow{DC}$=0可得
$\left\{\begin{array}{l}{{z}_{1}=0}\\{\sqrt{3}{x}_{1}-{y}_{1}=0}\end{array}\right.$令x1=1,则n2=(1,$\sqrt{3}$,0).
则cos<n1,n2>=$\frac{\sqrt{3}}{2\sqrt{2}}=\frac{\sqrt{6}}{4}$,
设二面角N-CE-D的平面角为θ,则sinθ=$\sqrt{1-(\frac{\sqrt{6}}{4})^{2}}=\frac{\sqrt{10}}{4}$,
∴二面角N-CE-D的正弦值为$\frac{\sqrt{10}}{4}$.…(12分)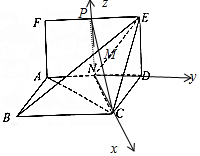
点评 本题考查了空间线线、线面位置关系,向量法求二面角,属于中档题,


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3) | B. | (-3,4] | C. | [3,4] | D. | (-∞,-3)∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com