
分析 以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,不妨设AB=2a,AD=2b,根据向量的坐标运算可得m=2ax,n=2by,再根据线性规划求出最大值.
解答 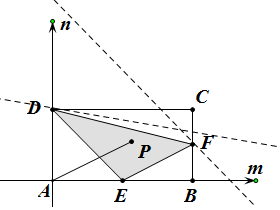 解:以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,
解:以AB,AD所在的直线为x,y轴,建立如图所示的坐标系,
不妨设AB=2a,AD=2b,
则A(0,0),B(2a,0),D(0,2b),
∵E、F分别为AB、BC的中点,
∴E(a,0),F(2a,b),
再设P(m,n),则0≤m≤2a,0≤n≤2b,
∵$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,
∴(m,n)=x(2a,0)+y(0,2b)=(2ax,2by),
∴m=2ax,n=2by,
∴设z=2x+3y=$\frac{m}{a}$+$\frac{3n}{2b}$,
∴n=-$\frac{2b}{3a}$m+$\frac{2b}{3}$z,
平移直线n=-$\frac{2b}{3a}$m+$\frac{2b}{3}$z,当与y轴上的截距最大时,此时z最大,
若经过点F(2a,b)时,最大,此时z=2a×$\frac{1}{a}$+$\frac{3}{2b}$×b=$\frac{7}{2}$,
若经过点D(0,b)时,最大,此时z=0×$\frac{1}{a}$+$\frac{3}{2b}$×2b=3,
综上所述2x+3y的最大值为$\frac{7}{2}$,
故答案为:$\frac{7}{2}$.
点评 本题考查了向量的坐标运算和和线性规划的问题,属于中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
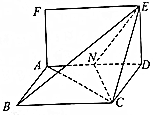 已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,点N时线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com