
分析 (1)利用正弦定理直接求解即可.
(2)利用三角形的面积公式求出b,然后求解c即可.
解答 解:(1)由 $\frac{a}{sinA}=\frac{c}{sinC}$,得$c=\frac{asinC}{sinA}=\frac{{2×\frac{{\sqrt{3}}}{2}}}{{\frac{{\sqrt{2}}}{2}}}=\sqrt{6}$.
(2)$S=\frac{1}{2}absinC$,即$\frac{1}{2}×2b×\frac{{\sqrt{3}}}{2}=\sqrt{3}$,得b=2
又a=2,$C=\frac{π}{3}$,故△ABC为等边三角形,所以c=2.
点评 本题考查正弦定理的应用,三角形的边长的求解,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 12 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c<0,则a+c<b+c | D. | 若$\sqrt{a}$<$\sqrt{b}$,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
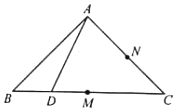 在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )| A. | 线段NO为定长 | B. | $|CO|∈[1,\sqrt{2})$ | C. | ∠AMO+∠ADB>180° | D. | 点O的轨迹是圆弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\overrightarrow b+\frac{1}{3}\overrightarrow c$ | B. | $\frac{1}{3}\overrightarrow b+\frac{2}{3}\overrightarrow c$ | C. | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}\overrightarrow b-\frac{2}{3}\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
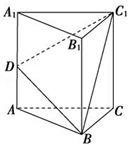 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
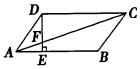
| A. | 54cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com