
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
【答案】
(1)解:由图象可知,周期T=2( ![]() ﹣
﹣ ![]() )=π,∴ω=
)=π,∴ω= ![]() =2
=2
∵点( ![]() ,0)在函数图象上,∴Asin(2×
,0)在函数图象上,∴Asin(2× ![]() +φ)=0
+φ)=0
∴sin( ![]() +φ)=0,∴
+φ)=0,∴ ![]() +φ=π+kπ,即φ=kπ+
+φ=π+kπ,即φ=kπ+ ![]() ,k∈z
,k∈z
∵0<φ< ![]()
∴φ= ![]()
∵点(0,1)在函数图象上,∴Asin ![]() =1,A=2
=1,A=2
∴函数f(x)的解析式为f(x)=2sin(2x+ ![]() )
)
(2)解:g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]﹣2sin[2(x+
]﹣2sin[2(x+ ![]() )+
)+ ![]() ]=2sin2x﹣2sin(2x+
]=2sin2x﹣2sin(2x+ ![]() )
)
=2sin2x﹣2( ![]() sin2x+
sin2x+ ![]() cos2x)=sin2x﹣
cos2x)=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() )
)
由﹣ ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈z
+2kπ,k∈z
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]()
∴函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间为[kπ﹣
)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ]k∈z
]k∈z
【解析】(1)先利用函数图象求此函数的周期,从而计算得ω的值,再将点( ![]() ,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;(2)先利用三角变换公式将函数g(x)的解析式化为y=Asin(ωx+φ)型函数,再将内层函数看做整体,置于外层函数即正弦函数的单调增区间上,即可解得函数g(x)的单调增区间
,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;(2)先利用三角变换公式将函数g(x)的解析式化为y=Asin(ωx+φ)型函数,再将内层函数看做整体,置于外层函数即正弦函数的单调增区间上,即可解得函数g(x)的单调增区间


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(Ⅱ)若直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
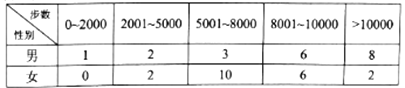
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
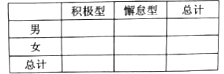
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附: 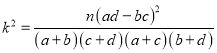 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() .
.
(1)求f(x)的解析式;
(2)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 的图象,给出下列命题:
的图象,给出下列命题:

①![]() 是函数
是函数![]() 的极值点
的极值点
②1是函数![]() 的极小值点
的极小值点
③![]() 在
在![]() 处切线的斜率大于零
处切线的斜率大于零
④![]() 在区间
在区间![]() 上单调递减
上单调递减
则正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的 ![]() ,则所得图象的函数解析式是( )
,则所得图象的函数解析式是( )
A.y=sin(4x+ ![]() π)
π)
B.y=sin(4x+ ![]() )
)
C.y=sin4x
D.y=sinx
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com