
| 3 |
| 5 |
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
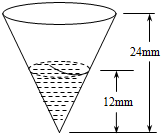 “降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为
“降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
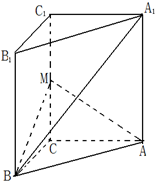 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com