
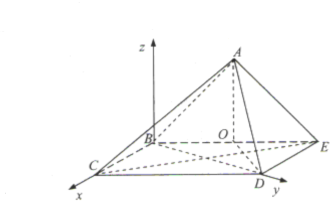
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| DE |
| AB |
| DE |
| ||||
|
|
-
| ||||||||
|
| 1 |
| 2 |
| AB |
| DE |
| n |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| BE |
|
| n |
| m |
| EA |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| EC |
|
| m |
| ||
| 2 |
| n |
| m |
|
| ||||
|
|
| 3 | ||
|
3
| ||
| 11 |
3
| ||
| 11 |


科目:高中数学 来源: 题型:
| A、使用了归纳推理 |
| B、使用了类比推理 |
| C、使用了“三段论”,但推理形式错误 |
| D、使用了“三段论”,但小前提错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:
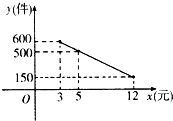 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
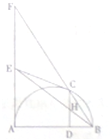 如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.
如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com