
函数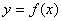 的定义域为
的定义域为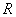 ,若存在常数
,若存在常数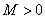 ,使得
,使得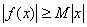 对一切实数
对一切实数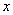
 均成立,则称
均成立,则称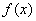 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数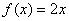 ,
,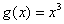 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若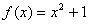 是“圆锥托底型”函数,求出
是“圆锥托底型”函数,求出 的最大值.
的最大值.
科目:高中数学 来源: 题型:
定义域为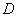 的函数
的函数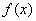 ,如果对于区间
,如果对于区间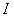 内
内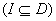 的任意两个数
的任意两个数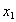 、
、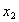 都有
都有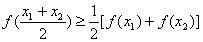 成立,则称此函数在区间
成立,则称此函数在区间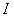 上是“凸函数”.
上是“凸函数”.
(1)判断函数 在
在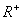 上是否是“凸函数”,并证明你的结论;
上是否是“凸函数”,并证明你的结论;
(2)如果函数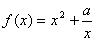 在
在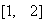 上是“凸函数”,求实数
上是“凸函数”,求实数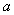 的取值范围;
的取值范围;
(3)对于区间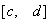 上的“凸函数”
上的“凸函数”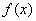 ,在
,在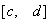 上任取
上任取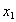 ,
,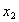 ,
, ,……,
,……,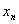 .
.
① 证明:当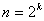 (
(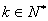 )时,
)时,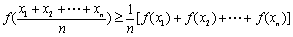 成立;
成立;
② 请再选一个与①不同的且大于1的整数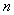 ,
,
证明: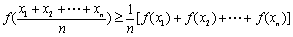 也成立.
也成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
在实数集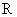 中,我们定义的大小关系“
中,我们定义的大小关系“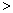 ”为全体实数排了一个“序”.类似的,我们在复数集
”为全体实数排了一个“序”.类似的,我们在复数集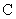 上也可以定义一个称为“序”的关系,记为“
上也可以定义一个称为“序”的关系,记为“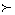 ”.定义如下:对于任意两个复数
”.定义如下:对于任意两个复数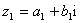 ,
,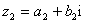 (
(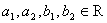 ),
),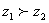 当且仅当“
当且仅当“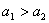 ”或“
”或“ 且
且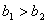 ”.
”.
按上述定义的关系“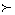 ”,给出如下四个命题:
”,给出如下四个命题:
①若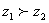 ,则
,则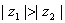 ;
;
②若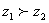 ,
,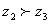 ,则
,则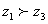 ;
;
③若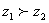 ,则,对于任意
,则,对于任意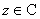 ,
,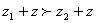 ;
;
④对于复数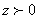 ,若
,若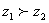 ,则
,则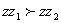 .
.
其中所有真命题的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是( )
A. A与C互斥 B. 任何两个均互斥
C. B与C互斥 D. 任何两个均不互斥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com