
分析 由题意结合函数图象可将问题转化为关于a的方程(3-a)2=$\frac{1}{4}$a2,解得即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{\frac{1}{16}x+\frac{1}{4}{a}^{2},x≥0}\\{{x}^{2}+({a}^{2}-4a+3)x+(3-a)^{2},x<0}\end{array}\right.$,
∴当x=0时,f(x)=$\frac{1}{4}$a2,
∵对任意的非零实数x1,存在唯一的实数x2(x2≠x1),使得f(x2)=f(x1)成立.
∴函数必须为连续函数,
∴(3-a)2=$\frac{1}{4}$a2,
解得a=2或a=6,
故答案为:2或6.
点评 本题主要考查分段函数的应用,结合一元二次函数的性质是解决本题的关键.综合性较强,注意利用数形结合进行求解,属中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
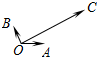 如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).
如图,平面内有三个向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为30°,且|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,|$\overrightarrow{OC}|=2\sqrt{3}$,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则(x,y)=(4,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com