

 ×AD×S△BCD=
×AD×S△BCD= ×(3-x)×
×(3-x)× ×x(3-x)=
×x(3-x)= (x3-6x2+9x)
(x3-6x2+9x) (x3-6x2+9x) x∈(0,3),
(x3-6x2+9x) x∈(0,3), (x-1)(x-3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
(x-1)(x-3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
 ,1,0),且
,1,0),且 =(-1,1,1)
=(-1,1,1) =(-
=(- ,λ-1,0)
,λ-1,0) •
• =0
=0 ,λ-1,0)=
,λ-1,0)= +λ-1=0,∴λ=
+λ-1=0,∴λ= ,∴N(0,
,∴N(0, ,0)
,0) 时,EN⊥BM
时,EN⊥BM =(x,y,z),由
=(x,y,z),由 及
及 =(-1,
=(-1, ,0)
,0) ,取
,取 =(1,2,-1)
=(1,2,-1) =(-
=(- ,-
,- ,0)
,0) ,
, >|=|
>|=| |=
|= =
=


科目:高中数学 来源: 题型:
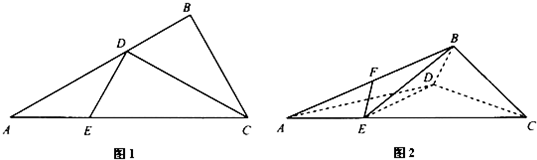
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)| x+1 |
| x-1 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
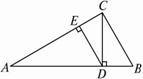
图-3-1
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
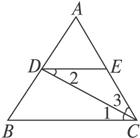
图
查看答案和解析>>
科目:高中数学 来源: 题型:
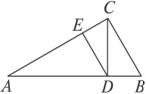
图
A.1 B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com