
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| a |
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| 2 |
| 1 |
| 2 |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| 2 |
| b |
| a |
| b |
| a |
| b |
| b |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
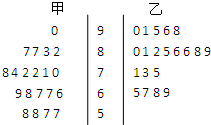 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| 3 |
| b-2c | ||
2cos(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| γ |
| β |
| γ |
| α |
| γ |
| β |
| γ |
| γ |
| α |
| γ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com