
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
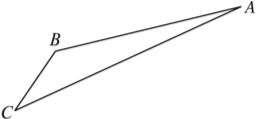
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
【答案】(1)1 040 m;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)在![]() 中,
中,
因为cos A=![]() ,cos C=
,cos C=![]() ,所以sin A=
,所以sin A=![]() ,sin C=
,sin C=![]() .
.
从而sin B=sin[π-(A+C)]=sin(A+C)
=sin Acos C+cos Asin C=![]() .
.
由正弦定理![]() ,可得
,可得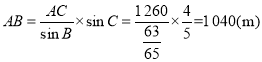 .
.
所以索道AB的长为1 040 m.
(2)假设乙出发t 分钟后,甲、乙两游客距离为d,
此时,甲行走了(100+50t)m,乙距离A处130t m,
所以由余弦定理,得![]() ,
,
因为![]() ,即0≤t≤8,所以当
,即0≤t≤8,所以当![]() 分钟时,甲、乙两游客距离最短.
分钟时,甲、乙两游客距离最短.
(3)由正弦定理![]() ,
,
得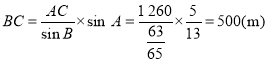 .
.
乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.
设乙步行的速度为v m/min,
由题意得![]() ,解得
,解得![]() ,
,
所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在![]() (单位:m/min)范围内.
(单位:m/min)范围内.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的通项公式是
的通项公式是![]() .
.
(1)判断![]() 是否是数列
是否是数列![]() 中的项;
中的项;
(2)试判断数列![]() 中的各项是否都在区间
中的各项是否都在区间![]() 内;
内;
(3)试判断在区间![]() 内是否有无穷数列
内是否有无穷数列![]() 中的项?若有,是第几项?若没有,请说明理由.
中的项?若有,是第几项?若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
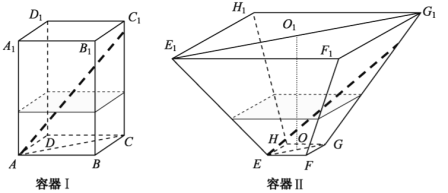
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 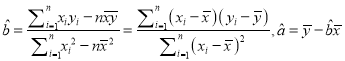 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为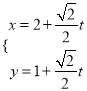 (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=log2(4x)log2(2x)的定义域为 ![]() . (Ⅰ)若t=log2x,求t的取值范围;
. (Ⅰ)若t=log2x,求t的取值范围;
(Ⅱ)求y=f(x)的最大值与最小值,并求取得最值时对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
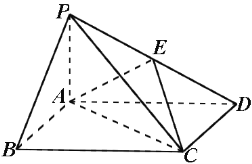
【题目】【2014高考课标2理数18】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com