
【题目】A={x|2x2﹣7x+3≤0},B={x||x|<a}
(1)当a=2时,求A∩B,A∪B;
(2)若(RA)∩B=B,求实数a的取值范围.
【答案】
(1)解:A={x|2x2﹣7x+3≤0}={x| ![]() ≤x≤3},B={x||x|<a};
≤x≤3},B={x||x|<a};
当a=2时,B={x|﹣2<x<2},
∴A∩B={x| ![]() ≤x<2},
≤x<2},
A∪B={x|﹣2<x≤3}
(2)解:∵CRA={x|x< ![]() 或x>3},
或x>3},
且(RA)∩B=B,
即B(RA);
当B=时,a≤0,满足题意;
当B≠时,a>0,
此时B={x|﹣a<x<a},
应满足0 ![]() ;
;
综上,实数a的取值范围是a≤ ![]()
【解析】(1)化简集合A,求出a=2时集合B,再计算A∩B和A∪B;(2)求出CRA,根据(RA)∩B=B得出B(RA), 讨论B=和B≠时,求出实数a的取值范围.
【考点精析】掌握集合的并集运算和集合的交集运算是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:现采用分层抽样的方法抽取容量为20的样本.
(1)其中课外体育锻炼时间在![]() 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?
(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在![]() 分钟内的概率.
分钟内的概率.
锻炼时间(分钟) |
|
|
|
|
|
|
人数 | 40 | 60 | 80 | 100 | 80 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+bx+c对于任意实数t都有f(2+t)=f(2﹣t),则f(1),f(2),f(4)的大小关系为( )
A.f(1)<f(2)<f(4)
B.f(2)<f(1)<f(4)
C.f(4)<f(2)<f(1)
D.f(4)<f(1)<f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1![]() 号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:
号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段: ![]() ;
; ![]() (单位:岁),其猜对歌曲名称与否的人数如图所示.
(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ)写出![]() 列联表;判断是否有
列联表;判断是否有![]() 的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(Ⅱ)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中恰好有一人在![]() 岁之间的概率.
岁之间的概率.
(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
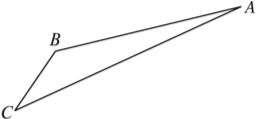
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润![]() 销售收入
销售收入![]() 成本)(附:对于一组数据
成本)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: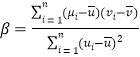 ,
,![]() ),
),![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知多面体![]() 如图所示.其中
如图所示.其中![]() 为矩形,
为矩形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,四边形
,四边形![]() 为梯形,且
为梯形,且![]() ,
, ![]() ,
, ![]() .
.

(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的余弦值等于
所成角的余弦值等于![]() ?若存在,请指出点
?若存在,请指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com