
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
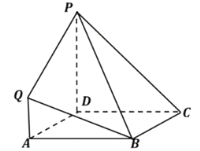
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由面面垂直的性质可得直线![]() 平面
平面![]() ,建立空间直角坐标系,表示出各点坐标后,求出平面
,建立空间直角坐标系,表示出各点坐标后,求出平面![]() 的一个法向量,直线
的一个法向量,直线![]() 的方向向量
的方向向量![]() ,由
,由![]() 即可得证;
即可得证;
(2)求出平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,利用
,利用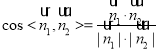 ,再利用同角三角函数的平方关系即可得解;
,再利用同角三角函数的平方关系即可得解;
(3)设![]() ,由题意
,由题意![]() 即
即![]() ,解出
,解出![]() 后即可得解.
后即可得解.
(1)证明:![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 直线
直线![]() 平面
平面![]() ,
,
由题意,以点![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正向建立如图空间直角坐标系,
轴的正向建立如图空间直角坐标系,
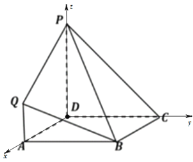
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
依题意易得![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
又![]() ,
,![]()
![]() ,
,
又![]() 直线
直线![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ;
;
(2)![]()
![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则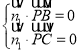 ,即
,即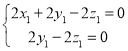 ,令
,令![]() 可得
可得![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则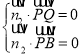 ,即
,即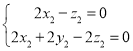 ,令
,令 ![]() 可得
可得![]() ,
,
![]()
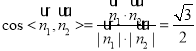 ,
,![]() 二面角
二面角![]() 的正弦值为
的正弦值为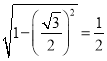 ;
;
(3)设![]() ,则
,则![]() ,又
,又![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
故所求线段![]() 的长为
的长为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象相邻的最高点之间的距离为
,其图象相邻的最高点之间的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,且
的图象,且![]() 为奇函数,则( )
为奇函数,则( )
A.![]() 的图象关于点
的图象关于点![]() 对称B.
对称B.![]() 的图象关于点
的图象关于点![]() 对称
对称
C.![]() 在
在![]() 上单调递增D.
上单调递增D.![]() 在
在![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】约公元前600年,几何学家泰勒斯第一个测出了金字塔的高度.如图,金字塔是正四棱锥,泰勒斯先测量出某个金字塔的底棱长约为230米;然后,他站立在沙地上,请人不断测量他的影子,当他的影子和身高相等时,他立刻测量出该金字塔影子的顶点A与相应底棱中点B的距离约为22.2米.此时,影子的顶点A和底面中心O的连线恰好与相应的底棱垂直,则该金字塔的高度约为( )
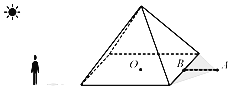
A.115米B.137.2米C.230米D.252.2米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019新型冠状病毒(2019―nCoV)于2020年1月12日被世界卫生组织命名.冠状病毒是一个大型病毒家族,可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.某医院对病患及家属是否带口罩进行了调查,统计人数得到如下列联表:
戴口罩 | 未戴口罩 | 总计 | |
未感染 | 30 | 10 | 40 |
感染 | 4 | 6 | 10 |
总计 | 34 | 16 | 50 |
(1)根据上表,判断是否有95%的把握认为未感染与戴口罩有关;
(2)从上述感染者中随机抽取3人,记未戴口罩的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: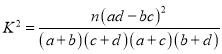 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了更好地应对新型冠状病毒肺炎疫情,对单位的职工进行防疫知识培训,所有职工选择网络在线培训和线下培训中的一种方案进行培训.随机抽取了140人的培训成绩,统计发现样本中40个成绩来自线下培训职工,其余来自在线培训的职工,并得到如下统计图表:
线下培训茎叶图在线培训直方图
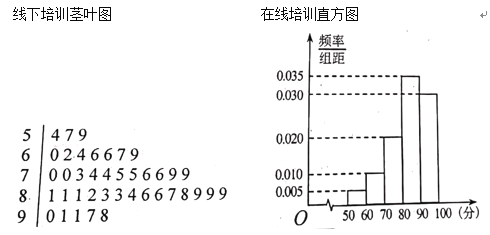
(1)得分90分及以上为成绩优秀,完成下边列联表,并判断是否有![]() 的把握认为成绩优秀与培训方式有关?
的把握认为成绩优秀与培训方式有关?
优秀 | 非优秀 | 合计 | |
线下培训 | |||
在线培训 | |||
合计 |
(2)成绩低于60分为不合格.在样本的不合格个体中随机再抽取3个,其中在线培训个数是![]() ,求
,求![]() 分布列与数学期望.
分布列与数学期望.
附: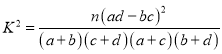 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com