
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,若点
,若点![]() 在曲线
在曲线![]() 位于第一象限的图象上运动,求四边形
位于第一象限的图象上运动,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 的焦点
的焦点![]() 到双曲线
到双曲线![]() 渐近线的距离为
渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以线段
两点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,且原点
,且原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
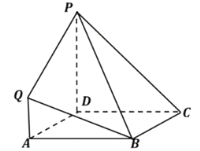
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com