
【题目】已知函数![]() (其中e是自然对数的底数,a,
(其中e是自然对数的底数,a,![]() )在点
)在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求函数![]() 的单调区间.
的单调区间.
(2)设函数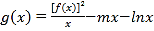 ,若
,若![]() 在
在![]() 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
【答案】(1)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() .由题意求出
.由题意求出![]() ,
,![]() ,即可求出
,即可求出![]() ,
,![]() ,代入
,代入![]() ,即可求出
,即可求出![]() 的单调区间;
的单调区间;
(2)由(1)知![]() .解法1:要使
.解法1:要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() 即可,利用导数求
即可,利用导数求![]() ;解法2:要使
;解法2:要使![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立.令
上恒成立.令![]() ,则只需
,则只需![]() 即可,利用导数求
即可,利用导数求![]() ;解法3:要使
;解法3:要使![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立. 先证明
上恒成立. 先证明![]() ,可得当
,可得当![]() 时,有
时,有![]() ,可得
,可得![]() ,即求实数m的取值范围.
,即求实数m的取值范围.
(1)对函数![]() 求导得
求导得![]() ,
,
由条件可知![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() .
.
![]() .令
.令![]() 得
得![]() ,
,
于是,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
故函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由(1)知![]() .
.
解法1:要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() 即可.
即可.
因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
因为当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,![]() 在
在![]() 上存在唯一的零点
上存在唯一的零点![]() ,满足
,满足![]() ,
,
所以![]() ,
,
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
于是![]()
由![]() 得
得![]() ,此时必有
,此时必有![]() ,
,![]() ,
,
两边同时取自然对数,则有![]() ,即
,即![]() .
.
构造函数![]() (
(![]() ),则
),则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,所以
,所以![]() ,即
,即![]() .
.
故![]() ,于是实数m的取值范围是
,于是实数m的取值范围是![]() .
.
解法2:要使![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立.
上恒成立.
令![]() (
(![]() ),则只需
),则只需![]() 即可.
即可.
![]() ,令
,令![]() (
(![]() ),则
),则![]() ,
,
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,![]() ,
,
所以![]() 有唯一的零点
有唯一的零点![]() ,且
,且![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
因为![]() ,两边同时取自然对数,则有
,两边同时取自然对数,则有![]() ,
,
即![]() .
.
构造函数![]() (
(![]() ),则
),则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() .
.
于是实数m的取值范围是![]()
解法3:要使![]() 在
在![]() 上恒成立,
上恒成立,
等价于![]() 在
在![]() 上恒成立.
上恒成立.
先证明![]() ,令
,令![]() (
(![]() ),则
),则![]() ,于是,当
,于是,当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增,所以
单调递增,所以![]() ,故
,故![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
所以,当![]() 时,有
时,有![]() ,所以
,所以![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取等号,于是实数m的取值范围是
时取等号,于是实数m的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】己知函数![]() 的定义域是
的定义域是![]() ,对任意的
,对任意的![]() ,有
,有![]() .当
.当![]() 时,
时,![]() .给出下列四个关于函数
.给出下列四个关于函数![]() 的命题:
的命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 是周期函数;
是周期函数;
③函数![]() 的全部零点为
的全部零点为![]() ,
,![]() ;
;
④当算![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有4个公共点.
的图象有且只有4个公共点.
其中,真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角三角形![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ;
;![]() .
.
(1)求角![]() 的大小;
的大小;
(2)在锐角三角形![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,求三角形
,求三角形![]() 的内角平分线
的内角平分线![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校对全体大一新生开展了一次有关“人工智能引领科技新发展”的学术讲座,随后对人工智能相关知识进行了一次测试(满分100分),如图所示是在甲、乙两个学院中各抽取的5名学生的成绩的茎叶图,由茎叶图可知,下列说法正确的是( )
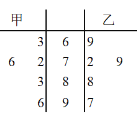
①甲、乙的中位数之和为159;
②甲的平均成绩较低,方差较小;
③甲的平均成绩较低,方差较大;
④乙的平均成绩较高,方差较小;
⑤乙的平均成绩较高,方差较大.
A.①②④B.①③④C.①③⑤D.②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值A,函数
处取得极值A,函数![]() ,其中
,其中![]() …是自然对数的底数.
…是自然对数的底数.
(1)求m的值,并判断A是![]() 的最大值还是最小值;
的最大值还是最小值;
(2)求![]() 的单调区间;
的单调区间;
(3)证明:对于任意正整数n,不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为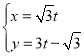 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com