
分析 由题意知这是一个古典概型,试验发生包含的事件数是6×6,要做出满足条件的事件数需要先计算出复数(m+ni)(n-mi)为实数时n和m的值,整理复数,使得它虚部为零,得到n=m,得到结果.
解答 解:由题意知这是一个古典概型,
试验发生包含的事件数是6×6=36,
而满足条件的事件是使得复数(m+ni)(n-mi)为实数,
先计算出复数(m+ni)(n-mi)为实数时n和m的值,
∵复数(m+ni)(n-mi)=2mn-(m2-n2)i为实数,
∴m2-n2=0,
∴m=n,
∴满足条件的事件数是6,
∴复数(m+ni)(n-mi)为实数的概率是$\frac{6}{36}$=$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 这是一个概率同复数结合的问题,是一个综合题,解题时需要先根据复数的条件得到概率中满足条件的事件数,虽是综合题,但本题的运算量不大,是一个基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
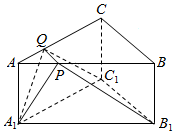 已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.
已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com