
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作出f(x)的函数图象,借助函数图象判断m的取值范围,根据函数的性质得出a+b=-2,cd=e4,利用基本不等式和函数单调性求出abcd,a+b+c+d的取值范围,求出两支图象斜率为-1的切线的截距,结合图象得出t的范围.
解答 解:作出f(x)的函数图象如图所示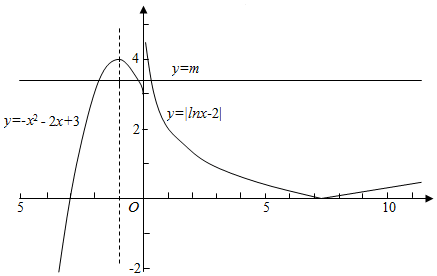
(1)由图象可知若y=m与f(x)的图象有四个交点,则3≤m<4,故①错误.
(2)∵y=-x2-2x+3关于直线x=-1对称,∴a<0,b<0,且a+b=-2,∴-a-b=2.
∴ab=(-a)(-b)<($\frac{-a-b}{2}$)2=1.
由lnc-2=-(lnd-2)得cd=e4.
∴0≤abcd<e4.故②正确.
(3)∵3≤m<4,∴3≤2-lnc<4,解得$\frac{1}{{e}^{2}}<c≤\frac{1}{e}$.
∴a+b+c+d=-2+c+$\frac{{e}^{4}}{c}$,
令g(c)=-2+c+$\frac{{e}^{4}}{c}$,则g′(c)=1-$\frac{{e}^{4}}{{c}^{2}}$.
∴当$\frac{1}{{e}^{2}}<c≤\frac{1}{e}$时,f′(c)<0,∴f(c)在($\frac{1}{{e}^{2}}$,$\frac{1}{e}$]上是减函数.
∴fmax(c)=f($\frac{1}{{e}^{2}}$)=e6+$\frac{1}{{e}^{2}}$-2,fmin(c)=f($\frac{1}{e}$)=e5+$\frac{1}{e}$-2.故③正确.
(4)由f(x)+x=t得f(x)=-x+t.
由方程f(x)+x=t恰有四个不同实根可知直线y=-x+t与y=-x2-2x+3(x≤0)有两个交点,
与y=|lnx-2|有两个交点.显然t≥3.
设y=-x2-2x+3的斜率为-1的切线为y=-x+t1,
则-2x-2=-1,解得x=-$\frac{1}{2}$.∴y=$\frac{17}{4}$.
∴t1=x+y=$\frac{15}{4}$>3.
设y=2-lnx的斜率为-1的切线为y=-x+t2.
则-$\frac{1}{x}=-1$,解得x=1,y=2.
∴t2=x+y=3.
∴3<t<$\frac{15}{4}$.故④错误.
故选B.
点评 本题考查了函数的零点个数判断,基本不等式,函数的最值,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.
如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
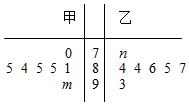 如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )
如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )| A. | a>b | B. | a<b | ||
| C. | a=b | D. | a,b的大小与m,n的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com