【题目】如图，
的外心为O，E是AC的中点，直线OE交AB于点D，M、N分别是
的外心、内心.若AB=2BC，证明：
为直角三角形.
【答案】见解析
【解析】
证法1：如图，由于点O、M皆在BC的中垂线上
设直线OM交BC于点P，交
于点F
则P是BC的中点，F是BC的的中点
因N是
的内心，所以，D、N、F三点共线，且
又OE是AC的中垂线，则DC=DA
而DF、OE为∠BDC的内、外角平分线，故
则OF为的直径，所以，OM=MF
又
，则NF=BF
作
于点H，于是
且
所以，
，故DN=BF=NF
因此，MN是
的中位线
从而，
而
，则
故
为直角三角形.
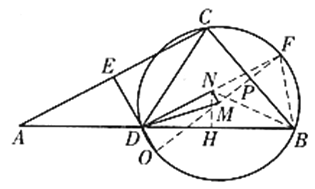
证法2：记
，
，
因DE是AC的中垂线，所以，AD=CD=b
有
①
延长DN交于点F，并记FN=e，DN=x
则FB=FC=FN=e
对圆内接四边形BDCF应用托勒密定理得
即
②
由式①、②得
故知N是弦DF的中点
而M为外心，所以，
故为直角三角形.
科目：高中数学 来源： 题型：
【题目】某超市在节日期间进行有奖促销，规定凡在该超市购物满400元的顾客，均可获得一次摸奖机会.摸奖规则如下：奖盒中放有除颜色不同外其余完全相同的4个球（红、黄、黑、白）.顾客不放回的每次摸出1个球，若摸到黑球则摸奖停止，否则就继续摸球.按规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励.
（1）求1名顾客摸球2次摸奖停止的概率；
（2）记X为1名顾客摸奖获得的奖金数额，求随机变量X的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）6个人按下列要求站一横排，甲、乙必须相邻，有多少种不同的站法？
（2）6个人按下列要求站一横排，甲不站左端，乙不站右端．有多少种不同的站法？
（3）用0，1，2，3，4，5这六个数字可以组成多少个六位数且是奇数（无重复数字的数）？
（4）用0，1，2，3，4，5这六个数字可以组成多少个个位上的数字不是5的六位数（无重复数字的数）？
查看答案和解析>>
科目：高中数学 来源： 题型：
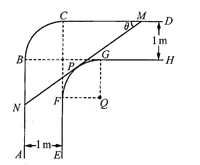
【题目】一走廊拐角处的横截面如图所示，已知内壁
和外壁
都是半径为1m的四分之一圆弧，
分别与圆弧
相切于
两点，
且两组平行墙壁间的走廊宽度都是1m.
（1）若水平放置的木棒
的两个端点
分别在外壁
和
上，且木棒与内壁圆弧相切于点
设
试用
表示木棒
的长度
（2）若一根水平放置的木棒能通过该走廊拐角处，求木棒长度的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
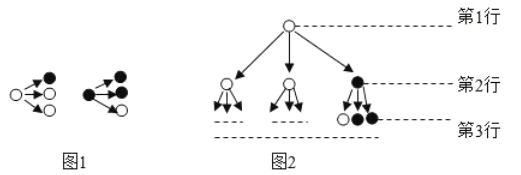
【题目】分形几何学是数学家伯努瓦．曼德尔布罗在20世纪70年代创立的一门新的数学学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照如图(1)所示的分形规律可得如图(2)所示的一个树形图．若记图(2)中第
行黑圈的个数为
，则
________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如表提供了工厂技术改造后某种型号设备的使用年限
和所支出的维修费
（万元）的几组对照数据：
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式：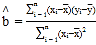
，
.
（1）若知道对呈线性相关关系，请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
