
在平面直角坐标系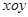 中,已知椭圆
中,已知椭圆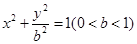 的左焦点为
的左焦点为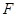 ,左、右顶点分别为
,左、右顶点分别为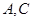 ,上顶点为
,上顶点为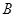 ,过
,过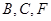 三点作圆
三点作圆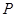
(Ⅰ)若线段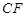 是圆
是圆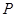 的直径,求椭圆的离心率;
的直径,求椭圆的离心率;
(Ⅱ)若圆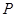 的圆心在直线
的圆心在直线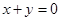 上,求椭圆的方程;
上,求椭圆的方程;
(Ⅲ)若直线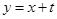 交(Ⅱ)中椭圆于
交(Ⅱ)中椭圆于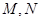 ,交
,交 轴于
轴于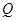 ,求
,求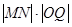 的最大值
的最大值
(Ⅰ)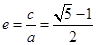 ;(Ⅱ)
;(Ⅱ)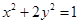 ;(Ⅲ)1
;(Ⅲ)1
解析试题分析:(Ⅰ)利用直径所对的圆周角是直角建立参数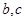 的关系,然后求之;(Ⅱ)利用圆心在直线
的关系,然后求之;(Ⅱ)利用圆心在直线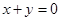 上寻找参数
上寻找参数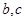 的关系,然后求之;(Ⅲ)直线与椭圆的相交问题采用设而不求的思路,利用坐标表示出
的关系,然后求之;(Ⅲ)直线与椭圆的相交问题采用设而不求的思路,利用坐标表示出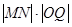 的表达式,然后使用基本不等式求解
的表达式,然后使用基本不等式求解
试题解析:(Ⅰ)由椭圆的方程知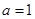 ,
,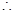 点
点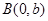 ,
,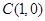 ,设F的坐标为
,设F的坐标为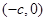 ,
,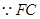 是
是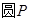 的直径,
的直径,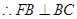 ,
,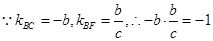 2分
2分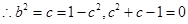 解得
解得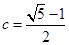 ,
, 椭圆离心率
椭圆离心率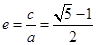 4分
4分
(Ⅱ)
 过点
过点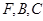 三点,
三点,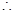 圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
FC的垂直平分线方程为 ①
①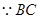 的中点为
的中点为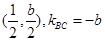 ,
,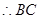 的垂直平分线方程为
的垂直平分线方程为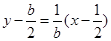 ②
②
由①②得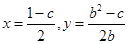 ,即
,即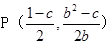 7分
7分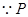 在直线
在直线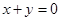 上,
上,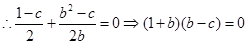 ,
,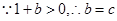 。
。
由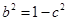 得
得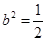 ,
,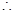 椭圆的方程为
椭圆的方程为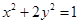 9分
9分
(Ⅲ)由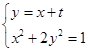 得
得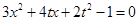 (*)
(*)
设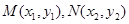 ,则
,则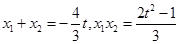
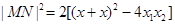
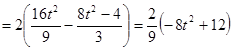 11分
11分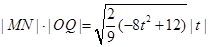
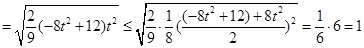 13分
13分
当且仅当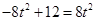 ,
,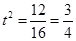 时取等号。此时方程(*)中的Δ>0,
时取等号。此时方程(*)中的Δ>0,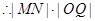 的最大值为1 13分
的最大值为1 13分
考点:直线与椭圆的位置关系


科目:高中数学 来源: 题型:解答题
已知一条曲线 在
在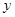 轴右边,
轴右边, 上每一点到点
上每一点到点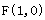 的距离减去它到
的距离减去它到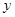 轴距离的差都等于1.
轴距离的差都等于1.
(1)求曲线C的方程;
(2)若过点M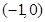 的直线
的直线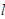 与曲线C有两个交点
与曲线C有两个交点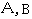 ,且
,且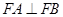 ,求直线
,求直线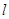 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知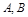 分别是椭圆
分别是椭圆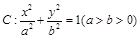 的左、右顶点,点
的左、右顶点,点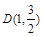 在椭圆
在椭圆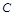 上,且直线
上,且直线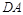 与直线
与直线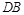 的斜率之积为
的斜率之积为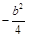 .
.
(Ⅰ)求椭圆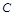 的方程;
的方程;
(Ⅱ)如图,已知 是椭圆
是椭圆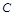 上不同于顶点的两点,直线
上不同于顶点的两点,直线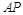 与
与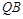 交于点
交于点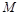 ,直线
,直线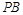 与
与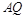 交于点
交于点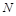 .① 求证:
.① 求证: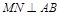 ;② 若弦
;② 若弦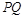 过椭圆的右焦点
过椭圆的右焦点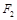 ,求直线
,求直线 的方程.
的方程.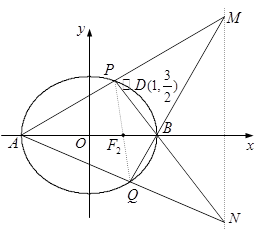
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A,B是椭圆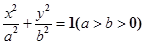 的两个顶点,
的两个顶点, 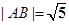 ,直线AB的斜率为
,直线AB的斜率为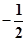 .求椭圆的方程;(2)设直线
.求椭圆的方程;(2)设直线 平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,
平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,
证明: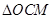 的面积等于
的面积等于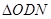 的面积.
的面积.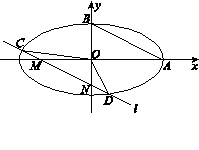
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆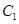 ,抛物线
,抛物线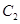 的焦点均在
的焦点均在 轴上,
轴上,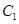 的中心和
的中心和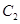 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
 |  | 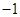 | 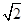 | 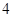 |
 | 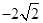 | 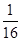 | 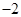 | 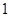 |
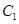 ,
,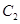 的标准方程;
的标准方程;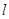 与
与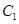 有且只有一个公共点
有且只有一个公共点 ,且与
,且与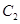 的准线交于
的准线交于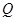 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点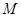 ,使得以
,使得以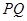 为直径的圆恒过点
为直径的圆恒过点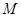 ?若存在,求出
?若存在,求出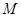 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设抛物线C: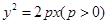 的焦点为F,经过点F的直线与抛物线交于A、B两点.
的焦点为F,经过点F的直线与抛物线交于A、B两点.
(1)若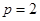 ,求线段
,求线段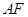 中点M的轨迹方程;
中点M的轨迹方程;
(2)若直线AB的方向向量为 ,当焦点为
,当焦点为 时,求
时,求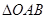 的面积;
的面积;
(3)若M是抛物线C准线上的点,求证:直线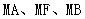 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
极坐标系与直角坐标系xOy有相同的长度单位,以原点D为极点,以x轴正半轴为极轴,曲线Cl的极坐标方程为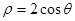 ,曲线C2的参数方程为
,曲线C2的参数方程为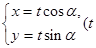 为参数)。
为参数)。
(1)当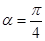 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标;
(2)若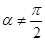 ,当
,当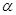 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,抛物线 的焦点为F,准线
的焦点为F,准线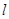 与x轴的交点为A.点C在抛物线E上,以C为圆心,
与x轴的交点为A.点C在抛物线E上,以C为圆心,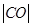 为半径作圆,设圆C与准线
为半径作圆,设圆C与准线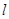 交于不同的两点M,N.
交于不同的两点M,N.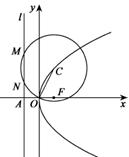
(I)若点C的纵坐标为2,求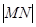 ;
;
(II)若 ,求圆C的半径.
,求圆C的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com