
分析 (Ⅰ)运用首项和递推式,可得a2,a3;
(Ⅱ)运用an+1-an=$\frac{{a}_{n}^{2}}{{n}^{2}}$,作差累加即可得证;
(Ⅲ)利用an+1>an、放缩可知$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$>-$\frac{1}{{n}^{2}}$,通过叠加可知$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$>-[$\frac{1}{(n-1)^{2}}$+…+$\frac{1}{{1}^{2}}$],n≥2,利用$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,并项相加可知an<$\frac{2n-1}{2n+1}$,;利用an<1放缩可知an+1<an+$\frac{{a}_{n}}{{n}^{2}}$,进而$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$<-$\frac{1}{{n}^{2}+1}$,通过叠加可知$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$<-[$\frac{1}{(n-1)^{2}+1}$+…+$\frac{1}{{1}^{2}+1}$],利用$\frac{1}{{n}^{2}+1}$>$\frac{1}{{n}^{2}+n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,并项相加可知an≥$\frac{n}{2n+1}$.
解答 (1)解:∵数列{an}满足a1=$\frac{1}{3}$,an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$,n∈N•.
∴a2=$\frac{1}{3}$+$\frac{1}{9}$=$\frac{4}{9}$,a3=a2+$\frac{{a}_{2}^{2}}{2}$=$\frac{4}{9}$+$\frac{1}{4}$•($\frac{4}{9}$)2=$\frac{40}{81}$.
(II)证明:∵an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$,n∈N•,
∴an+1-an=$\frac{{a}_{n}^{2}}{{n}^{2}}$,n∈N•,
∴a2-a1=$\frac{{a}_{1}^{2}}{{1}^{2}}$,a3-a2=$\frac{{a}_{2}^{2}}{{2}^{2}}$,…,an-an-1=$\frac{{a}_{n-1}^{2}}{(n-1)^{2}}$,
累加可得an-a1=$\frac{{a}_{1}^{2}}{{1}^{2}}$+$\frac{{a}_{2}^{2}}{{2}^{2}}$+…+$\frac{{a}_{n-1}^{2}}{(n-1)^{2}}$≥0,
∴an≥a1>0
∴数列{an}为正项数列,
∴an+1>an恒成立,
∴an+1-an=$\frac{{a}_{n}^{2}}{{n}^{2}}$>0,
∴数列{an}为递增数列;
(Ⅲ)证明:先证an≤$\frac{2n-1}{2n+1}$,
n=1时显然成立.
易知an>0,an+1-an=$\frac{{{a}_{n}}^{2}}{{n}^{2}}$>0,
∴an+1>an,
∴an+1=an+$\frac{{{a}_{n}}^{2}}{{n}^{2}}$<an+$\frac{{a}_{n}{a}_{n+1}}{{n}^{2}}$,
两端同时除以anan+1,得:$\frac{1}{{a}_{n}}$<$\frac{1}{{a}_{n+1}}$+$\frac{1}{{n}^{2}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$>-$\frac{1}{{n}^{2}}$,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$>-$\frac{1}{(n-1)^{2}}$,
…$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$>-$\frac{1}{{1}^{2}}$,
叠加得:$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$>-[$\frac{1}{(n-1)^{2}}$+…+$\frac{1}{{1}^{2}}$],n≥2.
又∵$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$>-($\frac{1}{n-2}$-$\frac{1}{n-1}$+…+$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{{1}^{2}}$)=-(2-$\frac{1}{n-1}$)=$\frac{1}{n-1}$-2,
又∵a1=$\frac{1}{3}$,
∴$\frac{1}{{a}_{n}}$-3>$\frac{1}{n-1}$-2,
∴$\frac{1}{{a}_{n}}$>$\frac{1}{n-1}$-2+3=1+$\frac{1}{n-1}$=$\frac{n}{n-1}$
∴an<$\frac{n-1}{n}$=1-$\frac{1}{n}$<1-$\frac{2}{2n+1}$=$\frac{2n-1}{2n+1}$;
再证an≥$\frac{n}{2n+1}$.
又a1=$\frac{1}{3}$≥$\frac{1}{2+1}$,
∵an<1,
∴an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$<an+$\frac{{a}_{n}}{{n}^{2}}$,
∴an>$\frac{{n}^{2}}{{n}^{2}+1}$•an+1,
∴an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$
=an+$\frac{{a}_{n}}{{n}^{2}}$•an
>an+$\frac{{a}_{n}}{{n}^{2}}$•$\frac{{n}^{2}}{{n}^{2}+1}$•an+1
=an+$\frac{1}{{n}^{2}+1}$•an•an+1,
两端同时除以anan+1,得:$\frac{1}{{a}_{n}}$>$\frac{1}{{a}_{n+1}}$+$\frac{1}{{n}^{2}+1}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$<-$\frac{1}{{n}^{2}+1}$,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$<-$\frac{1}{(n-1)^{2}+1}$,
…$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$<-$\frac{1}{{1}^{2}+1}$,
叠加得:$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$<-[$\frac{1}{(n-1)^{2}+1}$+…+$\frac{1}{{1}^{2}+1}$],
又∵$\frac{1}{{n}^{2}+1}$>$\frac{1}{{n}^{2}+n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$<-[$\frac{1}{{n}^{2}+1}$+$\frac{1}{(n-1)^{2}+1}$+…+$\frac{1}{{1}^{2}+1}$]
<-($\frac{1}{n-1}$-$\frac{1}{n}$+…+1-$\frac{1}{2}$)
=-(1-$\frac{1}{n}$),
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$=$\frac{1}{{a}_{n}}$-3<-(1-$\frac{1}{n}$),
∴$\frac{1}{{a}_{n}}$<3-1+$\frac{1}{n}$=$\frac{2n+1}{n}$,
∴an≥$\frac{n}{2n+1}$.
则$\frac{n}{2n+1}$≤an≤$\frac{2n-1}{2n+1}$,n∈N•.
点评 本题是一道关于数列递推关系的综合题,考查运算求解能力,利用放缩法和裂项是解决本题的关键,难度较大,注意解题方法的积累,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
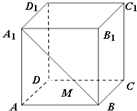 如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②
如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | ln 3 | C. | $\frac{1}{3ln3}$ | D. | $\frac{1}{ln3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
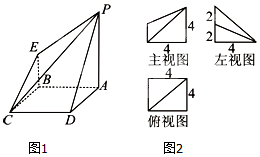 如图是一几何体的直观图、主观图、俯视图、左视图.
如图是一几何体的直观图、主观图、俯视图、左视图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
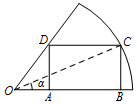 为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.
为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com