
分析 (1)求出函数的导数,得到函数的单调区间,从而求出函数的极大值即可;
(2)问题转化为a<${(3x{-x}^{2}-\frac{4}{x})}_{min}$,令h(x)=3x-x2-$\frac{4}{x}$,求出函数的导数,根据函数的单调性求出a的范围即可;
(3)根据f(a)≤f(6-b)?f(b)≤f(6-b)?$\frac{{e}^{6-b}}{{e}^{b}}≤\frac{{(6-b)}^{3}}{{b}^{3}}$,令3-b=t(t<0),得到(3-t)${e}^{\frac{2t}{3}}$-3-t≤0(*),令F(t)=(3-t)${e}^{\frac{2t}{3}}$-t-3(t<0),根据函数的单调性证明即可.
解答 解:(1)∵f′(x)=$\frac{{x}^{2}(3-x)}{{e}^{x}}$,令f′(x)=0,解得:x=3,
故f(x)在(-∞,3)递增,在(3,+∞)递减,
故x=3时,函数f(x)极大值=f(3)=$\frac{27}{{e}^{3}}$,无极小值;
(2)∵g(x)=3x2-x3,
∴3x2-x3>ax+b对任意的实数x∈[1,3]以及任意的实数b∈[2,4]恒成立,
∴3x2-x3-ax>b对任意的实数b∈[2,4]恒成立,
对任意的实数x∈[1,3]恒成立,
∴a<${(3x{-x}^{2}-\frac{4}{x})}_{min}$,
令h(x)=3x-x2-$\frac{4}{x}$,h′(x)=3-2x+$\frac{4}{{x}^{2}}$=$\frac{{3x}^{2}-{2x}^{3}+4}{{x}^{2}}$,
令φ(x)=3x2-2x3+4,φ′(x)=6x-6x2=6x(1-x)<0,
故φ(x)在(1,3)递减,∵φ(2)=0,
故h(x)在(1,2)递增,在(2,3)递减,
∵h(1)=-2,h(3)=-$\frac{4}{3}$,∴h(x)min=-2,
故a<-2;
(3)证明:由条件有f(a)=f(b),不妨设a<b,
则由(1)可知a<3<b,由于6-b<3,
从而f(a)≤f(6-b)?f(b)≤f(6-b)?$\frac{{e}^{6-b}}{{e}^{b}}≤\frac{{(6-b)}^{3}}{{b}^{3}}$,
令3-b=t(t<0),则$\frac{{e}^{3+t}}{{e}^{3-t}}$≤${(\frac{3+t}{3-t})}^{3}$,即${e}^{\frac{2t}{3}}$≤$\frac{3+t}{3-t}$?(3-t)${e}^{\frac{2t}{3}}$-3-t≤0(*),
令F(t)=(3-t)${e}^{\frac{2t}{3}}$-t-3(t<0),则F′(t)=-$\frac{4}{9}$t${e}^{\frac{2t}{3}}$,
∵t<0,故F′(t)>0,
故F(t)在(-∞,0)递增,从而F(t)<F(0)=0,
故F(t)在(-∞,0)递减,于是F(t)>F(0)=0,
这与(*)矛盾,
从而假设不成立,故a+b>6.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,考查函数恒成立问题,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{1}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
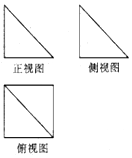 如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | $1+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com